Закон электромагнитной индукции. Правило Ленца — Мегаобучалка
Если электрический ток, как показали опыты Эрстеда, создает магнитное поле, то не может ли в свою очередь магнитное поле вызывать электрический ток в проводнике? Многие ученые с помощью опытов пытались найти ответ на этот вопрос, но первым решил эту задачу Майкл Фарадей (1791 — 1867).
В 1831 г. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает электрический ток. Этот ток назвали индукционным током.
Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки (рис. 192),
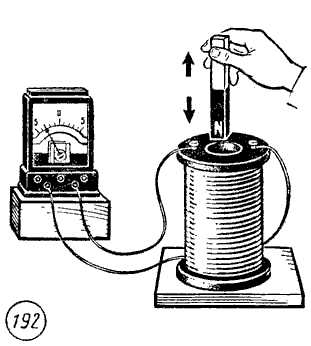
а также при изменении силы тока во второй катушке, магнитное поле которой пронизывает первую катушку (рис. 193).
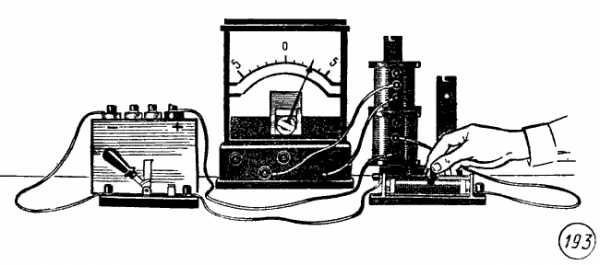
Явление возникновения электрического тока в замкнутом проводящем контуре при изменениях магнитного поля, пронизывающего контур, называется
Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или о возникновении ЭДС индукции.Количественное описание явления электромагнитной индукции дается на основе установления связи между ЭДС индукции и физической величиной, называемой магнитным потоком.
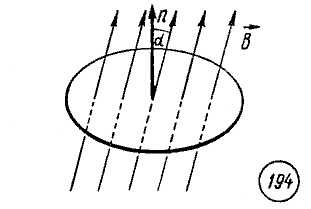
Магнитный поток. Для плоского контура, расположенного в однородном магнитном поле (рис. 194), магнитным потоком Фчерез поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь
. (54.1)
Правило Ленца. Опыт показывает, что направление индукционного тока в контуре зависит от того, возрастает или убывает магнитный поток, пронизывающий контур, а также от направления вектора индукции магнитного поля относительно контура. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено в 1833 г. Э. X. Ленцем.
Правило Ленца можно наглядно показать с помощью легкого алюминиевого кольца (рис. 195).
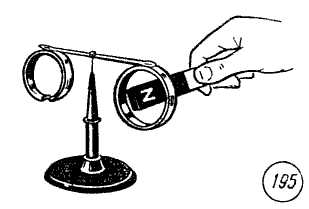
Опыт показывает, что при внесении постоянного магнита кольцо отталкивается от него, а при удалении притягивается к магниту. Результат опытов не зависит от полярности магнита.
Отталкивание и притяжение сплошного кольца объясняется возникновением индукционного тока в кольце при изменениях магнитного потока через кольцо и действием на индукционный ток магнитного поля. Очевидно, что при вдвигании магнита в кольцо индукционный ток в нем имеет такое направление, что созданное этим током магнитное поле противодействует внешнему магнитному полю, а при выдвигании магнита индукционный ток в нем имеет такое направление, что вектор индукции его магнитного поля совпадает по направлению с вектором индукции внешнего поля.
Закон электромагнитной индукции. Экспериментальное исследование зависимости ЭДС индукции от изменения магнитного потока привело к установлению закона электромагнитной индукции: ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.
В СИ единица магнитного потока выбрана такой, чтобы коэффициент пропорциональности между ЭДС индукции и изменением магнитного потока был равен единице. При этом закон электромагнитной индукции формулируется следующим образом: ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
.(54.2)
С учетом правила Ленца закон электромагнитной индукции записывается следующим образом:
.(54.3)
megaobuchalka.ru
Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Правило Ленца.
Явление электромагнитной индукции
Магнитным потоком Φ через площадь S контура называют величину
где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).
 |
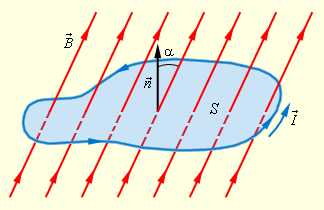| Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обхода контура связаны правилом правого буравчика |
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называетсявебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
| 1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
 |
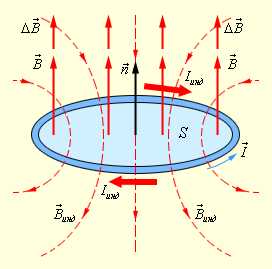| Рисунок 1.20.2. Иллюстрация правила Ленца. В этом примере а инд < 0. Индукционный ток Iиндтечет навстречу выбранному положительному направлению обхода контура |
Правило Ленца отражает тот экспериментальный факт, что инд и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Закон электромагнитной индукции
Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром.
В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n:
Но в общем случае, применяют формулу ЭДС с общим потокосцеплением:
ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в проводнике является катушка, через которую проходитпостоянный магнит. Направление индуцируемого тока можно определить с помощью правила Ленца.
Правило Ленца
Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.
В том случае, когда мы вводим магнит в катушку, магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца, направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.
В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.
Закон Ленца для электромагнитной индукции – HomeWork.net.ua
Индукционный ток создает собственное магнитное поле. Связь между направлением индукционного тока в контуре и индуцирующим магнитным полем была установлена Ленцем.
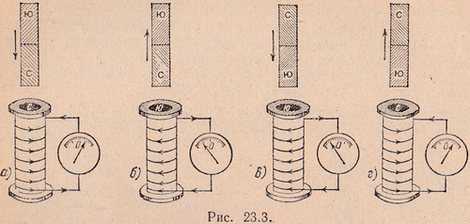
В опыте, изображенном на рис. 23.3, индукционный ток в соленоиде создает магнитное поле, полюсы которого указаны в отверстии соленоида. Проследив взаимодействие между магнитными полюсами соленоида и магнита во всех четырех случаях, приведенных на рисунке, и сравнив его с направлением движения магнита, можно видеть, что взаимодействие между полюсами всегда препятствует движению магнита. Ленцу удалось обобщить эту закономерность на все случаи электромагнитной индукции. Найденную им связь называют законом (правилом) Ленца для электромагнитной индукции: э. д. с. индукции создает в замкнутом контуре такой индукционный ток, который своим магнитным полем препятствует причине, вызывающей появление этой э. д. с.
Используя закон Ленца для определения направления индукционного тока, следует поступать следующим образом:
- найти причину, создающую индукционный ток;
- считая, что индукционный ток противодействует этой причине, найти направление его магнитного поля;
- определить направление индукционного тока по направлению его магнитного поля.
Приведем пример. Причиной, вызывающей появление индукционного тока во вторичной катушке при размыкании цепи первичной катушки (рис. 23.5), является исчезновение поля первичной катушки. Мешая этому исчезновению, индукционный ток во вторичной катушке должен создавать магнитное поле такого же направления, как у поля первичной катушки. Следовательно, направление индукционного тока во вторичной катушке будет совпадать с направлением тока, который протекал в первичной катушке до размыкания. (Покажите, что при замыкании цепи первичной катушки во вторичной возникает ток обратного направления.)
Из закона Ленца можно установить, что энергия индукционного тока в проводнике получается за счет той энергии, которая затрачивается на преодоление противодействия магнитного поля индукционного тока. Например, если разомкнуть цепь катушки, изображенной на рис. 23.3, и подсчитать работу, нужную для того, чтобы вставить в нее и вынуть магнит определенное число раз, а затем повторить этот опыт при замкнутой цепи, то во втором случае работа будет заметно больше, чем в первом. Это объясняется тем, что в первом случае собственного магнитного поля вокруг катушки нет, так как в ней нет тока, а во втором случае поле есть. Лишняя работа во втором случае идет на преодоление противодействия этого поля и равна энергии индукционного тока в катушке. Нетрудно видеть, что с помощью явления электромагнитной индукции можно превращать механическую энергию в электрическую, а также передавать электрическую энергию из одной цепи в другую.
Когда индукционный ток возникает вследствие какого-либо механического движения, то электрическая энергия получается за счет механической. Такое превращение энергии происходит в индукционных генераторах, установленных на электростанциях. Когда же индукционный ток возникает при отсутствии механического движения, то электрическая энергия переходит из одной цепи в другую. Такая передача энергии происходит в трансформаторах.
Явлением электромагнитной индукции объясняют диамагнитный эффект. Когда вещество попадает в магнитное поле, на каждый движущийся по орбите электрон начинает действовать сила Лоренца, которая увеличивает или уменьшает (в зависимости от направления вращения электрона) центростремительную силу, действующую на электрон. Это приводит к изменению орбиты и частоты обращения электрона, что равносильно уменьшению или увеличению кругового тока, соответствующего движению электрона по орбите, причем получается, что круговые токи электронов усиливаются, если их магнитные поля направлены против внешнего поля, и уменьшаются, если они направлены по полю.
Таким образом, если в отсутствие внешнего поля круговые токи электронов в молекуле диамагнетика уравновешивают друг друга, и молекула не имеет магнитного момента, то во внешнем поле это равновесие нарушается и возникает результирующий магнитный момент молекулы, направленный против внешнего поля. Этот результат, вообще говоря, прямо следует и из закона Ленца: изменение круговых токов в молекуле является индукционным током, и его магнитное поле должно быть направлено против вызвави1вго его внешнего поля.
Диамагнитный эффект возникает во всех веществах, но если молекулы вещества имеют собственные магнитные моменты, которые ориентируются по направлению внешнего магнитного поля и усиливают его, то диамагнитный эффект перекрывается более сильным парамагнитным эффектом и вещество оказывается парамагнетиком.
Сильный диамагнитный эффект наблюдается при сверхпроводимости. Когда сверхпроводник попадает в магнитное поле, в нем, как и в обычном проводнике, наводятся индукционные токи, но, в отличие от молекулярных индукционных токов, их образуют свободные электроны. В сверхпроводнике эти индукционные токи не встречают сопротивления и циркулируют, пока существует внешнее магнитное поле, противодействуя его проникновению внутрь сверхпроводника. Сверхпроводники, как и все диамагнетики, выталкиваются из магнитного поля.
homework.net.ua
Закон Фарадея. Правило Ленца. Максвеловская трактовка явления электромагнитной индукции
Зако́н электромагни́тной инду́кции Фараде́яявляется основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.Закон гласит: Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.
Согласно закону электромагнитной индукции Фарадея (в СИ):
где -электродвижущая сила, действующая вдоль произвольно выбранного контура,
-магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца:Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток. (противоположен возбуждающему поку)
Cогласно идее Максвелла изменяющееся со временем магнитное поле порождает электрическое поле. Это поле существенно отличается от порождаемого неподвижными зарядами электростатического поля. Электростатическое поле потенциально, его силовые линии начинаются и заканчиваются на зарядах. Электрическое поле, создаваемое переменным магнитным полем вихревое, его силовые линии замкнуты.
В 1865 г. Максвелл высказал гипотезу о том, что изменение электрического поля должно вызывать образование магнитного поля. В дальнейшем эта гипотеза нашла экспериментальное подтверждение.
Переменное электрическое поле, которое может создавать переменное магнитное поле, Максвелл назвал током смещения.
13.Явление взаимо и самоиндукции. Токи Фуко.
Взаимоиндукция (взаимная индукция)— возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, “натянутую” на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).
Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.
Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1]при изменении протекающего через контур тока.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем)
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока :
Коэффициент пропорциональности называется коэффициентом самоиндукции или индуктивностью контура (катушки).
Вихревые токи или токи Фуко́ — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.
Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и т. п., а также в некоторых конструкциях поездов, для торможения.
Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нём возникают вихревые токи, разогревающие его до плавления.
С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.
Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.
Энергия магнитного поля
Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна
где I — сила тока в контуре.
Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Ток смещения
Ток смещения или абсорбционный ток — величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.
Введение тока смещения позволило устранить противоречие в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.
Ток смещения не являетсяэлектрическим током, но измеряется в тех же единицах, что и электрический ток.
infopedia.su
33. Закон электромагнитной индукции (закон Фарадея). Правило Ленца. Токи Фуко и их применение.
Закон Фарадея можно сформулировать таким образом: ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: .
Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающему этот индукционный ток. Значение индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.
Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми. Их также называют токами Фуко — по имени первого исследователя. Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного
потока, индуцирующему вихревые токи. Вихревые токи помимо торможения вызывают нагревание проводников. Поэтому для уменьшения потерь на нагревание якоря генераторов и сердечники трансформаторов делают не сплошными, а изготовляют из тонких пластин, отделенных одна от другой слоями изолятора, и устанавливают их так, чтобы вихревые токи были направлены поперек пластин. Джоулева теплота, выделяемая токами Фуко, используется в индукционных металлургических печах. Если сплошные проводники нагревать токами высокой частоты, то в результате скин-эффекта происходит нагревание только их поверхностного слоя. На этом основан метод поверхностной закалки металлов. Меняя частоту поля, он позволяет производить закалку на любой требуемой глубине. Токи высокой частоты практически текут в тонком поверхностном слое, то провода для них делаются полыми.
34. Явление самоиндукции. Индуктивность. Взаимная индукция. Взаимная индуктивность.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого пропорциональна току. Сцепленный с контуром магнитный поток поэтому пропорционален току в контуре: , где — коэффициент пропорциональности, называемый индуктивностью контура.
Индуктивность бесконечно длинного соленоида: .
Единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб (вебер).
Рассмотрим
два неподвижных контура (1
и
2), расположенных достаточно близко друг
от друга и
.
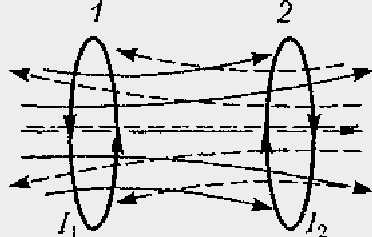
Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности и называютсявзаимной индуктивностью контуров. Коэффициенты и зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды. Эти коэффициенты будут равны между собой, если среда не ферромагнитная.
studfiles.net
Закон электромагнитной индукции. Правило Ленца
Глава 16. Электромагнитная индукция.
Мы знаем, что электрическое поле в проводнике создаёт ток, а ток порождает магнитное поле. Таким образом, электрическое поле создаёт магнитное поле. Но справедливо и обратное утверждение – с помощью магнитного поля можно создать электрическое поле.
Экспериментально это доказывается опытами Фарадея. Если вносить и выносить магнит в катушку, соединённую с амперметром, то через амперметр будет течь электрический ток (рис. 16.1). Если же магнит внести в катушку и оставить его неподвижно, то тока не будет. Впервые этот опыт проделал М.Фарадей в 1831г.
Это явление было названо электромагнитной индукцией (индукция – значит наведение). Ток, возникающий при электромагнитной индукции, называют индукционным.
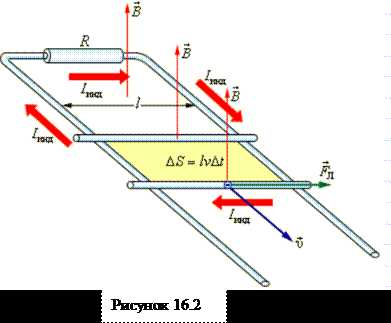Рассмотрим возникновение ЭДС индукции, а следовательно, и индукционного тока. Пусть проводник без тока длиной ℓ движется в магнитном поле со скоростью υ (рис.16.2). Магнитное поле однородно. Вектор магнитной индукции однородного магнитного поля В. При движении проводника свободные электроны, содержащиеся в нём, будут также двигаться в туже сторону, т.е. возникает конвекционный ток. Направление этого тока противоположно направлению движения электронов. На каждый движущийся электрон со стороны магнитного поля действует сила Лоренца Fл. Электроны под действием этой силы движутся слева направо и в правой части проводника длиной ℓ будут накапливаться отрицательные заряды, а в левой – положительные. В результате этого образуется разность потенциалов φ1 –φ2; таким образом в проводнике возникает электрическое поле напряжённостью Е, которое препятствует дальнейшему перемещению электронов.
Заряды перестают перемещаться при такой напряжённости Е электрического поля, когда сила Fэ=еЕ, действующая со стороны электрического поля, будет равна по модулю, но противоположна по направлению силе Fл=еВυ, действующая со стороны магнитного поля:
Fэ= Fэ
еЕ=- еВυ или Е=- Вυ
Напряжённость Е электрического поля в движущемся проводнике длиной ℓ и разность потенциалов φ1 –φ2 связаны между собой соотношением:
φ1 –φ2 =Еℓ
или
φ1 –φ2 =- Вυ ℓ
Если такой проводник замкнуть, то по цепи пойдёт ток.
Таким образом, на концах проводника длиной ℓ, движущегося со скоростью υ в однородном магнитном поле В индуцирует ЭДС
εинд=- Вυ ℓ (16.1)
Учитывая, что υ =dx/dt , где х перемещение проводника, преобразуем формулу
(16.2)
(Idx =dS – площадь контура, охватываемая проводником длиной ℓ при движении за промежуток времени dt). Тогда
(16.3)
BdS = dФ
Следовательно,
(16.4)
ЭДС индукции в замкнутом контуре равна скорости изменения пронизывающего его магнитного потока, взятой с противоположным знаком(закон электромагнитной индукции, или закон Фарадея).
Если замкнутый контур содержит N последовательно соединённых витков (например катушка или соленоид), то ЭДС индукции равна сумме ЭДС каждого витка:
(16.5)
Согласно Максвеллу, поле покоящегося магнита является чисто магнитным:
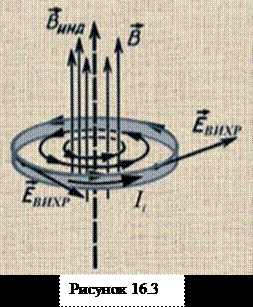В≠ 0, Е=0. поле движущегося магнита (или переменного тока) уже перестаёт быть таковым: у него и В≠ 0, Е≠ 0. это означает что, как только магнитное поле В начинает изменяться ( в результате движения магнита или изменения силы тока в цепи), сразу же возникает и электрическое поле Е. Это поле в отличие от электростатического не связано непосредственно с электрическими зарядами, и потому его силовые линии не могут на них ни начинаться, ни кончаться; они представляют собой замкнутые кривые, охватывающие линии магнитного поля (рис.16.3). Поля с замкнутыми силовыми линиями, как мы знаем, называются вихревыми.
Таким образом, переменное магнитное поле порождает вихревое электрическое поле.
Для поддержания электрического тока в цепи необходимо стороннее поле. Таким полем как раз и является вихревое электрическое. Роль сторонних сил выполняет сила Лоренца, под действием которой происходит разделение зарядов, в результате чего на концах проводника появляется разность потенциалов. Вихревое электрическое поле непотенциально и потому характеризуется ЭДС индукции. ЭДС индукции в проводнике является работой по перемещению единичного положительного заряда вдоль проводника.
Используя закон Ома для полной цепи и закон Фарадея, получаем выражение для индукционного тока:
(16.6)
Из этого уравнения следует, что индукционный ток зависит от сопротивления контура.
Можно ли заранее предсказать в каком направлении пойдёт индукционный ток.
Рассмотрим два случая:
1. Магнит приближается к катушке (dФ > 0) (рис.16.4, а). В процессе приближения магнита к катушке действует сила отталкивания, которая тормозит его падение. Это следует из закона сохранения энергии:
Когда в катушки появляется индукционный ток, то вместе с ним возникает и его собственное магнитное поле В. Это поле и отталкивает приближающийся магнит. Поскольку такое отталкивание возможно лишь в том случае, когда магнит и катушки обращены друг к другу одноимёнными полюсами, то сверху у катушки должен быть северный магнитный полюс (N). Зная это с помощью правой руки можем определить и направление индукционного тока в катушке. Индукционный ток в этом случае считаем отрицательным.
2. Магнит удаляется от катушки dФ < 0 (рис.16.4 б). При удалении магнита от катушки на него начинает действовать сила притяжения, препятствующая его подъёму. Такое возможно лишь в том случае, когда магнит и катушки с появившимся в нём индукционным током оказываются обращёнными друг к другу разноимёнными полюсами. Индукционный ток в этом случае направлен в противоположную сторону и сила тока положительна.
В каждом из двух случаев обнаруживается определённое противодействие попыткам изменить расстояние между катушкой и магнитом.
Направление индукционного тока определяется по правилу Ленца:
Индукционный ток всегда имеет такое направление, при котором возникает противодействие причинам, его породившим.
Знак минус в законе Фарадея отражает закон Ленца.
При возрастании магнитного потока , εинд < 0, I < 0; при уменьшении магнитного потока , εинд > 0, I > 0.
Самоиндукция
После того как удалось «превратить магнетизм в электричество», Фарадей обнаружил, что при подключении цепи, содержащей катушку с сердечником (рис.16.5), к источнику постоянного напряжения сила тока устанавливается не сразу, а постепенно (рис.16.6). Аналогичное явление наблюдалось и при отключении цепи от источника. В этом случае ток также прекращался постепенно, а не мгновенно (рис.16.7).
Ток, продолжающий идти в цепи и после отключения её от источника напряжения, получил название экстратока размыкания.
В результате проведённых исследований Фарадей понял, что наблюдаемый эффект является частным случаем электромагнитной индукции и представляет собой «индуктивное влияние электрического тока на самого себя».
Современная теория описанных явлений сводится к следующему. Когда электрический ток в цепи изменяется (например, увеличивается при замыкании цепи или уменьшается при её размыкании), то изменяется и создаваемое этим током магнитное поле. Изменяя, это поле порождает вихревое электрическое поле, которое и влияет на силу тока в данной цепи. В этом и заключается «действие электрического тока самого на себя».
Возникновение вихревого электрического поля в проводящем контуре при изменении силы тока в нём же самом называется самоиндукцией.
ЭДС электромагнитной индукции, которая возникает в контуре при изменении силы тока в нём, называется ЭДС самоиндукции.
ЭДС самоиндукции определяется из закона Фарадея:
(16.7)
Магнитный поток, сцеплённый с контуром, всегда пропорционален силе тока в нём:
Ф = LI (16.8)
Коэффициент пропорциональности L называется индуктивностью контура или коэффициентом самоиндукции.
v Единица индуктивности – генри.
Индуктивность зависит от формы и размеров соленоида, а также от магнитных свойств окружающей среды.
Поскольку самоиндукция является частным случаем электромагнитной индукции, то эту ЭДС самоиндукции можно найти по закону:
(16.9)
Если контур представляет собой соленоид, содержащий N витков, то
(16.10)
(dψ – потокосцепление)
Таким образом, чем больше индуктивность цепи и чем быстрее изменяется в ней сила тока, тем большая ЭДС самоиндукции и, следовательно, вихревое электрическое поле в ней возникают.
В соответствии с правилом Ленца возникающее при самоиндукции вихревое электрическое поле имеет такое направление, при котором возникает противодействие тому изменению силы тока в цепи, которое его вызвало. Это означает, что при увеличении силы тока (ΔІ˃0) напряжённость появившегося вихревого электрического поля будет направлена противоположно току (мешая ему нарастать), а при уменьшении силы тока (ΔІ˂0) она будет направлена в ту же сторону, что и ток (препятствуя его убыванию)
При размыкании цепи возникает индукционный ток, идущий в том же направлении, что и основной, поэтому сила тока изменяется очень быстро. При значительной индуктивности это может привести к тому, что в цепи возникает ЭДС самоиндукции, значительно превышающая ЭДС источника тока. При этом на концах разомкнутой цепи появится настолько большая разность потенциалов, что наступит электрический пробой воздуха и в месте размыкания цепи проскочит искра. Этим можно объяснить и то, что лампочки перегорают именно в момент выключения света.
Ø Определим индуктивность соленоида.
Напряжённость поля во всех точках внутри соленоида одинакова и равна H=In, где n – число витков N, приходящихся на единицу длины соленоида ℓ (N/ℓ). Если общее число витков соленоида равно N, то . Магнитный поток, пронизывающий один виток соленоида, равен
(16.11)
(S – площадь поперечного сечения соленоида; μ – относительная магнитная проницаемость окружающей среды).
Полный магнитный поток равен потокосцеплению:
(16.12)
Так как Sℓ = V (объём соленоида), то
(16.13)
Поэтому индуктивность соленоида
или (16.14)
studopedya.ru
§3. Закон электромагнитной индукции. Правило Ленца — Phystech.Academy
Пусть произвольный контур с током находится во внешнем магнитном поле. Из принципа суперпозиции магнитных полей и определения магнитного потока следует, что полный магнитный поток `”Ф”`, пронизывающий контур, состоит из потока от внешнего поля `”Ф”_”внеш”` и потока от собственного поля `”Ф”_”соб”`:
`”Ф”=”Ф”_”внеш”+”Ф”_”соб”`. (3)
При этом внешний магнитный поток `”Ф”_”внеш”` может изменяться со временем как из-за изменения внешнего магнитного поля во времени (в каждой точке поля индукция внешнего магнитного поля зависит от времени), так и из-за движения контура или отдельных его частей. Собственный магнитный поток `”Ф”_”соб”` может тоже меняться со временем в результате изменения тока в контуре по каким-либо причинам и в результате изменения индуктивности контура (при его деформации, например).
Опытным путём установлено, что независимо от причин, вызывающих изменение полного магнитного потока через контур, в контуре возникает электродвижущая сила, называемая электродвижущей силой индукции:
`=-(d”Ф”)/(dt)`. (4)
Здесь направление нормали к контуру и положительное направление обхода контура, связанные друг с другом правилом буравчика, определяют знак `”Ф”` и ЭДС индукции положительна, если направление её действия совпадает с положительным направлением обхода контура, и отрицательна в противном случае. Под направлением действия ЭДС на некотором участке цепи будем понимать направление действия вдоль этого участка сторонних сил на положительные заряды, т. е. то направление, в котором потечёт ток через участок цепи с ЭДС при мысленном замыкании этого участка резистором.
Равенство (4) и представляет собой математическую запись закона электромагнитной индукции Фарадея. Производную `(d”Ф”)/(dt)` называют скоростью изменения магнитного потока.
Из равенств (3) и (4) получаем:
`=-(d”Ф”_”внеш”)/(dt)-(d”Ф”_”соб”)/(dt)`. (5)
Слагаемое `-(d”Ф”_”внеш”)/(dt)` представляет собой ЭДС индукции, возникающую из-за изменения внешнего магнитного потока. Если собственное поле можно не учитывать (пренебрегать индуктивностью), то ЭДС индукции в контуре определяется только первым слагаемым. Ещё раз подчеркнём, что это слагаемое обусловлено как изменением внешнего поля во времени, так и движением контура или его частей во внешнем поле.
Слагаемое
`=-(d”Ф”_”соб”)/(dt)=-(d(LI))/(dt)=-L(dI)/(dt)-I(dL)/(dt)` (6)
называется ЭДС самоиндукции, т. к. оно появляется благодаря изменению во времени собственного магнитного потока через контур. Напомним, что изменение собственного магнитного потока может происходить как за счёт изменения тока (по каким-либо причинам), так и за счёт изменения индуктивности контура.
Если индуктивность остаётся постоянной во времени, то равенство (6) принимает вид:
`=-L(dI)/(dt)`. (7)
Затронем часто встречающийся при решении задач вопрос о том, пренебрегать или нет индуктивностью контура. Этот вопрос в каждом конкретном случае должен решаться отдельно на основании вклада, даваемого в общую ЭДС каждым слагаемым в формуле (5). Чаще всего индуктивностью контура в виде одного витка или рамки, состоящей из малого числа витков, можно пренебречь. А вот индуктивностью контура, состоящего из значительного числа витков, например катушки, пренебрегать не стоит. Одним из критериев для оценки роли индуктивности может служить сравнение величин внешнего магнитного поля и собственного поля контура, а точнее, сравнение изменений величин этих полей за время наблюдения.
Заметим, что в формуле (4) знаки ЭДС индукции и изменения магнитного потока `d”Ф”` противоположны: если `d”Ф”>0`, то `<0`, и наоборот. Противоположность знаков этих двух величин, обеспеченная присутствием в формуле (4)
знака «`-`», отражает правило Ленца: ЭДС индукции всегда направлена так, чтобы пытаться препятствовать причине, вызвавшей индукцию.
Северный полюс магнита удаляется от проводящего кольца (рис. 3). Определить направление индукционного тока в кольце. Куда направлена сила, действующая на кольцо?
Для ответа на первый вопрос удобно за причину, вызывающую ЭДС индукции в кольце, взять уменьшение магнитного потока через кольцо. По правилу Ленца собственное поле, созданное индукционным током, должно препятствовать этому уменьшению. Поэтому собственное поле в плоскости кольца и внутри кольца направлено туда же, что и внешнее, т. е. вправо. По правилу буравчика индукционный ток в кольце направлен против часовой стрелки, если смотреть на кольцо справа.
Для ответа на второй вопрос удобнее за причину, вызывающую ЭДС индукции, взять увеличение расстояния между магнитом и кольцом. По правилу Ленца появится противодействие этой причине, т. е. между кольцом и магнитом возникнет сила притяжения. И чем больше индукционный ток, тем больше будет сила притяжения. Итак, на кольцо действует сила, направленная к магниту.
Катушка сопротивлением `R=40` Ом и индуктивностью `L=0,01` Гн замкнута накоротко и находится во внешнем магнитном поле (рис. 4). Начиная с определённого момента, внешнее поле начинает изменяться. В результате за некоторое время магнитный поток внешнего поля через катушку возрос на `0,002` Вб, а ток достиг значения `0,08` А. Какой заряд прошёл за это время по катушке?
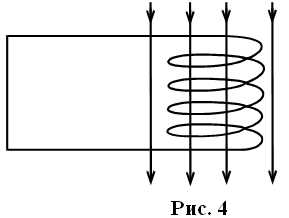
Изменяющееся внешнее поле вызывает в катушке ЭДС индукции, в результате чего возникает изменяющийся со временем ток, являющийся причиной появления ЭДС самоиндукции. Свяжем направление нормали к витку катушки и положительное направление обхода витка правилом буравчика. Этим будет задаваться связь между знаками магнитного потока, тока и обеих ЭДС в контуре. Разобьём всё время на сколь угодно малые интервалы `Deltat_i`. Пусть за время `Deltat_i` магнитный поток от внешнего поля изменился на величину `Delta”Ф”_i`, а ток изменился на величину `DeltaI_i`. Тогда по закону Ома для замкнутой цепи
`-(Delta”Ф”_i)/(Deltat_i)-L(DeltaI_i)/(Deltat_i)=I_iR`. (8)
Здесь `I_i` – среднее значение тока в катушке в течение времени `Deltat_i`. Умножив обе части равенства (8) на `Deltat_i` и учтя, что `I_iDeltat_i` есть протёкший через катушку заряд `Deltaq_i` за время `Deltat_i`, получаем:
`-Delta”Ф”_i-LDeltaI_i=RDeltaq_i`. (9)
Сложив равенства вида (9) для всех `Deltat_i`, получаем:
`-sum_i Delta”Ф”_i-Lsum_i DeltaI_i=Rsum_i Deltaq_i`.
Поскольку `sum_i Deltaq_i=q` – протёкший через катушку за время опыта заряд, `sum_i Delta”Ф”_i=Delta”Ф”` – полное изменение потока внешнего поля через катушку, `sum_i DeltaI_i=DeltaI` – а полное изменение тока в катушке за время опыта, то имеем: `-Delta”Ф”-LDeltaI=Rq`. Так как ток в момент начала изменения внешнего магнитного поля равен нулю, то `DeltaI=I_”кон”-0=I_”кон”`. Здесь `I_”кон”` – значение тока в конце опыта. Итак,
`q=-(Delta”Ф”+LI_”кон”)/R`.
Если направление нормали к витку катушки выбрать таким, чтобы `Delta”Ф”` было положительным, т. е. равным `0,002` Вб, то значение `I_”кон”` надо взять отрицательным, т. е. равным `-0,08` А. Это следует из правила Ленца: знак индукционного тока должен быть противоположен знаку изменения магнитного потока, вызвавшего этот ток. Таким образом, `Delta”Ф”=0,002` Вб, `I_”кон”=-0,08` А,
`q=-(Delta”Ф”+LI_”кон”)//R=-3*10^(-5)` Кл.
Знак «минус» у заряда означает, что он прошёл в отрицательном направлении обхода витка катушки.
phystech.academy