2.3. Третий закон Ньютона.
Понятие силы определено как мера взаимодействия тел, т.е. при рассмотрении движения какого-нибудь тела учитывается только одна сторона этого взаимодействия. Ясно, однако, что все тела надо рассматривать как равноправные, т.е. если второе тело воздействует на первое, то и первое тело воздействует на второе. Третий закон Ньютона устанавливает соотношение между этими воздействиями: Силы, с которыми два тела действуют друг на друга, равны по величине и направлены пр одной прямой в разные стороны.
Пример: книга лежит на столе; она притягивается к Земле и вследствие этого давит на стол. Однако книга не проваливается к центру Земли, т.к. стол со своей стороны действует на книгу с силой равной по величине силе давления книге на стол. Эта сила со стороны стола носит название реакции опоры. К самой книге приложено две силы: сила притяжения и сила реакции опоры. Они равны по величине и противоположно направлены, т.е. их сумма равна нулю, поэтому книга никуда не двигается.
2.4. Импульс. Закон сохранения импульса.
Импульсом принято называть величину .
Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т1, m2, . .., тn и ,, .. .,. Пусть ,, …,— равнодействующие внутренних сил, действующих на каждое из этих тел,a , , …,— равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из
,
,
………………
.
Складывая почленно эти уравнения, получим
.
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
или
(2-4)
где импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (рассматриваем замкнутую систему)
.
т.е. . (2-5)
Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются
законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса —
studfiles.net
§ 2.3. Третий закон Ньютона
Воздействие тел, друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой F12 , то тело 1 действует на тело 2 с силой F21. Третий закон Ньютона утверждает, что силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению, т.е.
Таким образом, силы всегда возникают попарно. Подчеркиваем, что силы, фигурирующие в сотношении (2.6) приложены к разным телам; поэтому они не могут уравновесить друг друга.
Третий закон Ньютона, как и первый два, справедлив лишь в инерциальных системах отсчета. В неинерциальных системах отсчета этот закон оказывается несправедливым.
§ 2.4. Силы
Чтобы свести нахождение закона движения частицы к чисто математической задаче, необходимо прежде всего – в соответствии с уравнением (2.2) – знать действующую на частицу силу, т.е. зависимость силы от определяющих ее величин. Каждая такая зависимость получена в конечном счете на основании обработки результатов опыта и, по существу, всегда опирается на уравнение (2.2), как на определение силы.
Наиболее фундаментальные силы, лежащие в основе всех механических явлений, – это силы гравитационные и электрические. Приведем выражения для этих сил в самом простом виде, когда взаимодействующие массы (заряды) покоятся или движутся с малой (нерелятивистской) скоростью.
Сила гравитационного притяжения, действующая между двумя материальными точками. В соответствии с законом всемирного тяготения эта сила пропорциональная произведению масс точек m1 и m
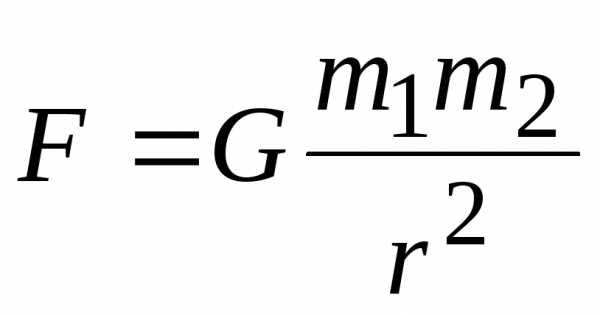 , (2.7)
, (2.7)
где G – гравитационная постоянная.
Фигурирующие в этом законе массы называют гравитационными в отличие от инертной массы, входящей во второй закон Ньютона. Из опыта, однако, установлено, что гравитационная и инертная массы любого тела строго пропорциональны друг другу. Поэтому можно считать их равными (т.е. выбрать один и тот же эталон для измерения обеих масс) и говорить просто о
Кулоновская сила, действующая между двумя точечными зарядами q1 и q2
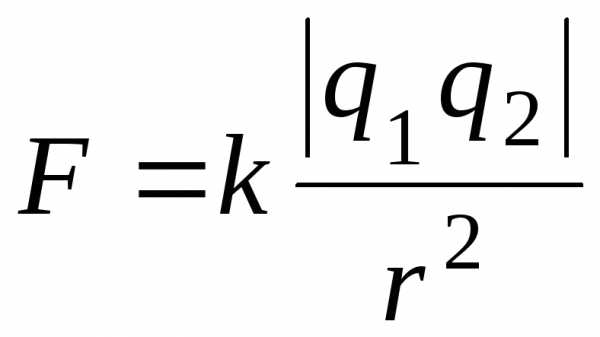 , (2.8)
, (2.8)
где r –расстояние между зарядами,
k – коэффициент
пропорциональности, зависящий от выбора
системы единиц. В системе СИ 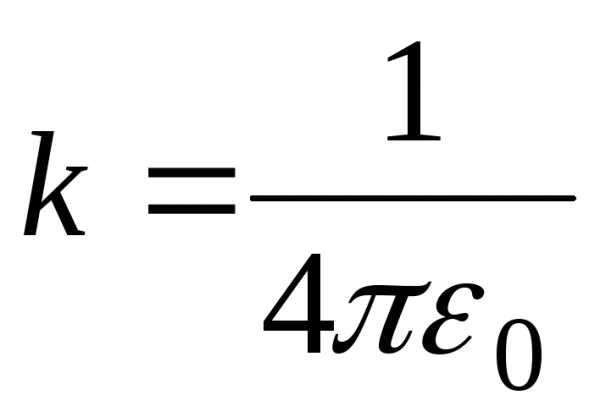 ,
где 0 — электрическая постоянная.
,
где 0 — электрическая постоянная.
В отличие от гравитационной силы кулоновская сила может быть как силой притяжения, так и силой отталкивания.
Заметим, что закон Кулона (2.8) перестает выполняться точно, если заряды движутся. Электрическое взаимодействие движущихся зарядов оказывается сложным образом зависящим от их движения. Одну из частей этого взаимодействия, обусловленную движением, называют магнитной силой (отсюда и другое название данного взаимодействия – электромагнитное). При малых (нерелятивистских) скоростях магнитная сила составляет пренебрежимо малую часть электрического взаимодействия и оно с высокой степенью точности описывается законом (2.8).
Несмотря на то, что гравитационные и электрические взаимодействия лежат в основе всего бесчисленного разнообразия механических явлений, анализ явлений, особенно макроскопических оказался бы весьма сложным, если бы во всех случаях мы исходили из этих фундаментальных взаимодействий. Поэтому удобно ввести другие, приближенные, силы (которые в принципе могут быть получены из фундаментальных сил). Это необходимо для того, чтобы упростить математически задачу настолько, чтобы ее можно было практически решить. С этой целью вводят, например, следующие силы.
studfiles.net
2.3. Второй закон ньютона
ma=F.
Не следует воспринимать эту формулировку как определение силы. Смысл её совершенно иной. Второй закон Ньютона утверждает, что в инерциальных системах отсчёта сила, действующая на тело, всегда равна произведению массы этого тела на ускорение, вызванное силой.
С другой стороны, используя эталонную массу, можно ввести единицу измерения силы именно на основе второго закона Ньютона.
Если известны силы, действующие на тело массой
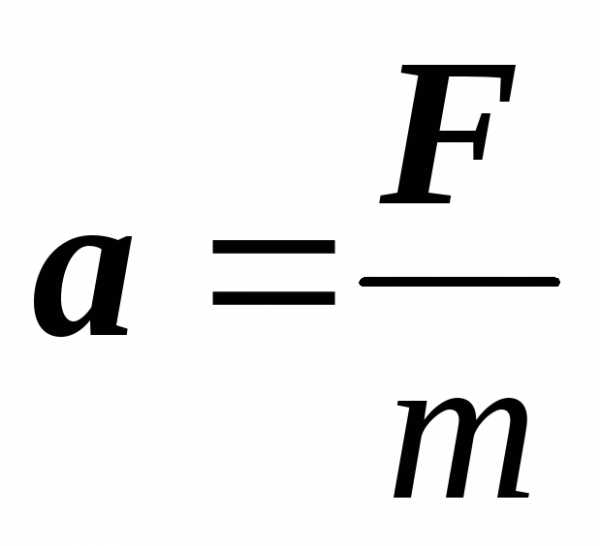 ,
можно получить зависимость скорости
от времени, а проинтегрировав уравнение
зависимости скорости от времени –
выражение, описывающее зависимость
координаты от времени.
,
можно получить зависимость скорости
от времени, а проинтегрировав уравнение
зависимости скорости от времени –
выражение, описывающее зависимость
координаты от времени. Например, пусть ускорение тела постоянно a=constи направлено вдоль осих; в начальный
момент тело покоится в точке с координатойх=0. По определению ускорение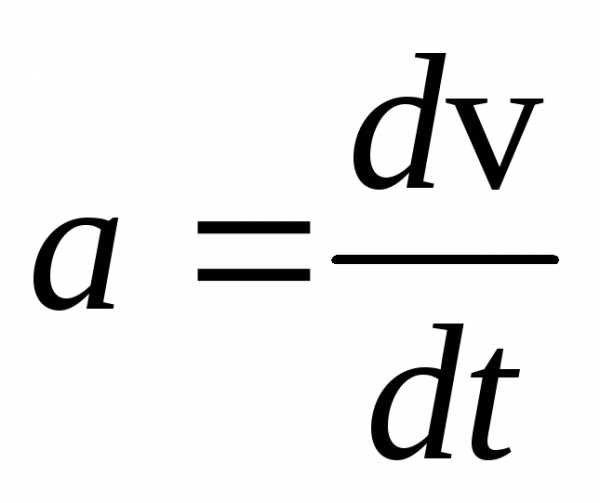 .
Отсюдаdv=adtи
.
Отсюдаdv=adtи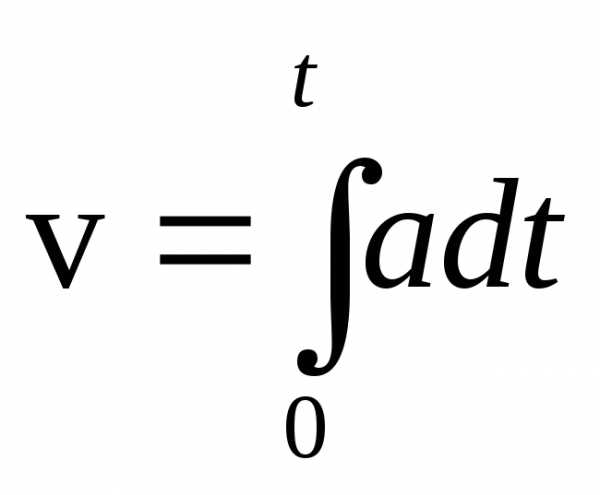 .
Взяв интеграл, получаем уравнение
зависимостискорости тела от
времениv=at.
.
Взяв интеграл, получаем уравнение
зависимостискорости тела от
времениv=at.
По определению скорость 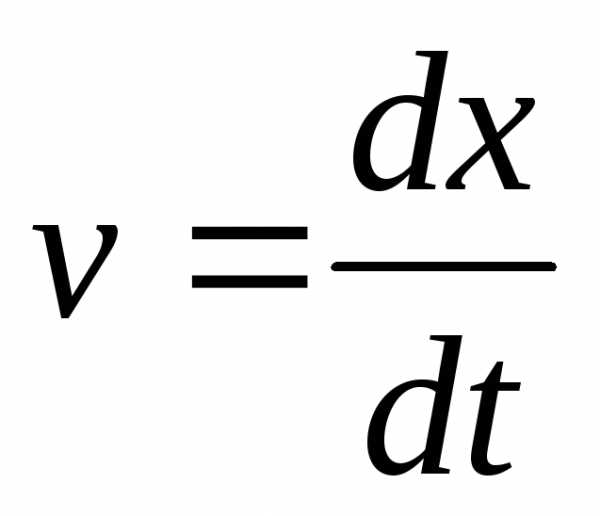 .
Тогдаdx=vdt=atdtи
.
Тогдаdx=vdt=atdtи 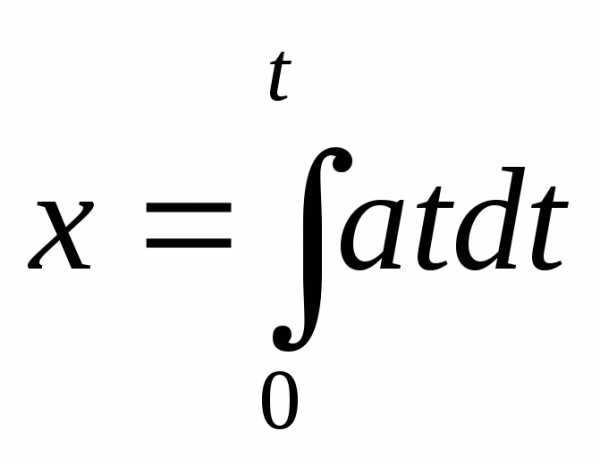 ..
Взяв интеграл, получим уравнение,
..
Взяв интеграл, получим уравнение,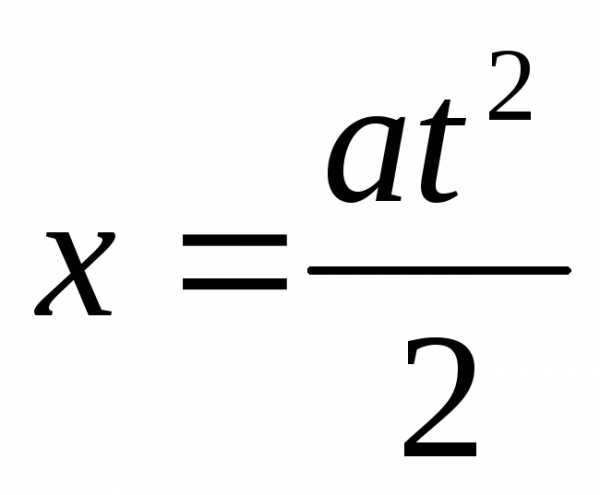 ,
описывающее зависимость координаты
тела от времени.
,
описывающее зависимость координаты
тела от времени.
Таким образом, зная силы, действующие на тело, можно предсказать, как будет двигаться тело под действием этих сил, в какой момент времени тело окажется в нужной точке пространства (кроме сил необходимо также знать начальное положение тела и его начальную скорость).
Второй закон Ньютона можно сформулировать и иначе: скорость изменения импульса тела равна сумме действующих на тело сил:
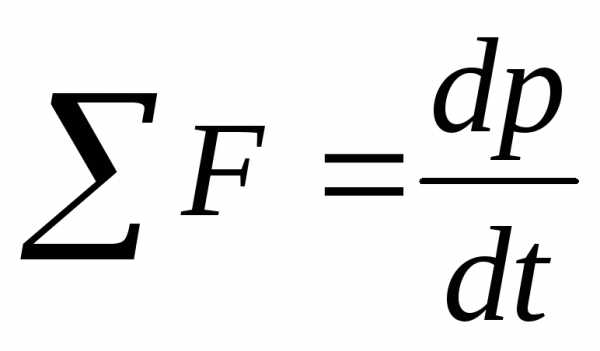 .
.
Эта формулировка не отвергает рассмотренную ранее. Обе формулировки отображают одну и ту же закономерность, они взаимосвязаны, что видно изследующего:
.
Второй закон Ньютона часто называют основным законом динамикипоступательного движения. Именно на основе второго закона решается основная задача динамики – описание движения тел под действием сил, приложенных к телу.
2.4 Третий закон Ньютона
Первый и второй законы Ньютона рассматривают движение тел. Третий закон рассматривает взаимодействие двух тел. Он гласит:силы, с которыми действуют друг на друга два взаимодействующих тела, всегда равны другдругу по величине и направлены в противоположные стороны
F12=-F21
Обратите внимание: силыF12 иF21 приложены к разным телам. Это означает, что эти силы не компенсируют друг друга.
Третий закон справедлив для сил любой природы. Все виды фундаментальных взаимодействий порождают равные по величине и противоположные по направлению силы одной природы.
2.5. Принцип относительности галилея
Как было показано в разд. 2.1, любая система отсчёта, движущаяся равномерно и прямолинейно относительно инерциальной системы отсчёта, является инерциальной.
В разделе 1.6 рассматривалось, что если системы отсчёта движутся друг относительно друга равномерно и прямолинейно, то ускорение тела, измеренное в каждой из систем отсчёта, будет одинаковым.
Это означает, что ускорение какого-либо тела, измеренное в разных инерциальных системах отсчёта, будет одинаковым.
Из второго закона Ньютона следует, что
ускорение тела массой т зависит
от величины силы, приложенной к телу: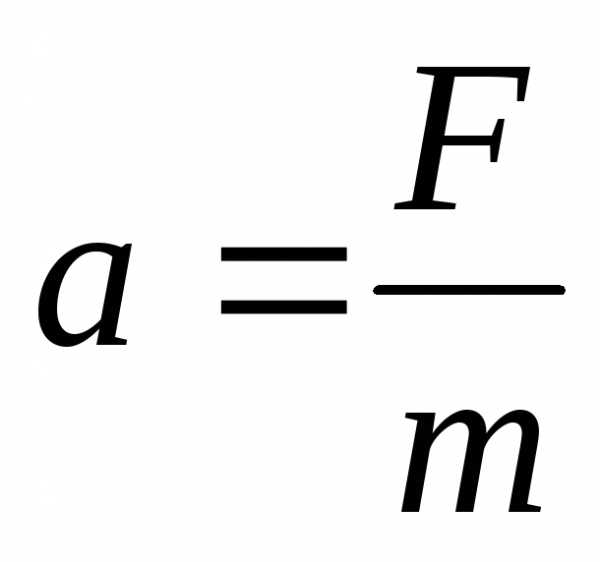 .
Тогда во всех инерциальных системах
отсчёта на рассматриваемое телодействует одна и та же сила.
.
Тогда во всех инерциальных системах
отсчёта на рассматриваемое телодействует одна и та же сила.
Следовательно, динамические уравнения, составленные в разных системах отсчёта для одного и того же тела, во всех инерциальных системах отсчёта имеют абсолютно одинаковый вид. По виду такого уравнения совершенно невозможно определить, в какой именно инерциальной системе отсчёта производились измерения.
Следовательно, в инерциальных системах отсчёта все механические процессы протекают одинаково; все инерциальные системы по своим свойствам эквивалентны, абсолютной инерциальной системы отсчёта не существует. Эту формулировку и принято называтьпринципом относительности Галилея.
studfiles.net
2.3. Третий закон Ньютона
Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль прямой, соединяющей эти точки: F12= –F21, где F12 – сила, действующая на первую материальную точку со стороны второй; F21 – сила, действующая на вторую точку со стороны первой. Эти силы приложены к разным телам, всегда действуют парами и являются силами одной природы.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек: для системы материальных точек взаимодействие можно свести к силам парного взаимодействия между материальными точками.
Силы, подчиняющиеся трем законам Ньютона, называются ньютоновскими силами.
2.4.Закон сохранения импульса
Рассмотрим механическую систему – совокупность материальных точек, рассматриваемых как единое целое (m1, m2,…,mn – их массы, v1, v2,…,vn – их скорости). Силы взаимодействия между материальными точками системы называются внутренними (F1, F2,…Fn – равнодействующие внутренних сил, действующих на каждую из материальных точек). Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними (F1, F2,…Fn – равнодействующие внешних сил, действующих на каждую из материальных точек). Согласно третьему закону Ньютона, силы, действующие между материальными точками механической системы равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна нулю Fi = 0. Тогда второй закон Ньютона для механической системы имеет вид dp/dt=(d/dt)mivi=Fi, где p=mivi – импульс системы.
Механическая система, на которую не действуют внешние силы, называется замкнутой (изолированной). Следовательно, для изолированной (замкнутой) системы имеем выражение dp/dt=0 или p=mivi=const которое выражает закон сохранения импульса: импульс замкнутой (изолированной) системы не изменяется с течением времени. Закон сохранения импульса справедлив для любой замкнутой системы частиц, и он является фундаментальным законом природы. Закон сохранения импульса является следствием однородности пространства – при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются (иными словами, физические свойства и законы движения замкнутой системы не зависят от выбора положения начала координат инерциальной системы отсчета).
2.5.Силы трения
Из опыта известно, что тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил, с течением времени замедляет свое движение и останавливается. Это объясняется существованием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения могут быть различной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.
Различают внешнее (сухое) и внутреннее (жидкое, вязкое) трение. Внешнее трение возникает в плоскости касания двух тел при их относительном перемещении, и оно обусловлено шероховатостью соприкасающихся поверхностей (или обусловлено силами межмолекулярного взаимодействия, если поверхности очень гладкие). Если тела неподвижны, то говорят о трении покоя. Если тела движутся, то говорят о трении скольжения, качения или верчения.
Для силы скольжения имеет место экспериментальный закон Fтр = fN,
где N – сила нормального давления , f – коэффициент трения скольжения , зависящий от свойств соприкасающихся поверхностей. Для уменьшения трения скольжения используют смазку, которая заполняет неровности между поверхностями и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга – внешнее трение скольжения заменяется на значительно меньшее внутреннее трение жидкости. Другой способ уменьшения силы трения– замена трения скольжения на трение качения (шариковые и роликовые подшипники).
Для силы трения качения справедлив экспериментальный закон Fтр = fкN/r,
где r – радиус катящегося тела, fк – коэффициент трения качения.
studfiles.net
2.3. Третий закон Ньютона
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
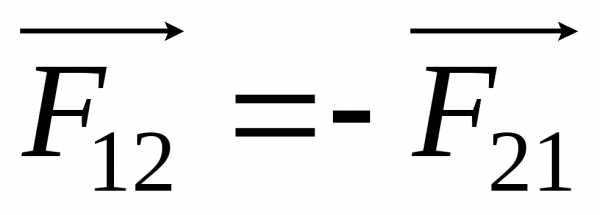 ,
(2.10)
,
(2.10)
где – сила, действующая на первую материальную
точку со стороны второй;  – сила, действующая на вторую материальную
точку со стороны первой. Эти силы
приложены к разным материальным точкам
(телам), всегда действуют парами и
являются силами одной природы.
– сила, действующая на вторую материальную
точку со стороны первой. Эти силы
приложены к разным материальным точкам
(телам), всегда действуют парами и
являются силами одной природы.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
2.4. Силы в механике
Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в механике мы будем рассматривать различные силы: трения, упругости, тяготения.
 а) Силы
трения. Из
опыта известно, что всякое тело, движущееся
по горизонтальной поверхности другого
тела, при отсутствии действия на него
других сил с течением времени замедляет
свое движение и в конце концов
останавливается. Это можно объяснить
существованием силы
трения,
которая препятствует скольжению
соприкасающихся тел друг относительно
друга. Различают внешнее (сухое) и
внутреннее (жидкое или вязкое) трение. Внешним
трением называется
трение, возникающее в плоскости касания
двух соприкасающихся тел при их
относительном перемещении. Если
соприкасающиеся тела неподвижны друг
относительно друга, говорят о трении
покоя, если
же происходит относительное перемещение
этих тел, то в зависимости от характера
их относительного движения говорят о трении
скольжения, качения или верчения.
а) Силы
трения. Из
опыта известно, что всякое тело, движущееся
по горизонтальной поверхности другого
тела, при отсутствии действия на него
других сил с течением времени замедляет
свое движение и в конце концов
останавливается. Это можно объяснить
существованием силы
трения,
которая препятствует скольжению
соприкасающихся тел друг относительно
друга. Различают внешнее (сухое) и
внутреннее (жидкое или вязкое) трение. Внешним
трением называется
трение, возникающее в плоскости касания
двух соприкасающихся тел при их
относительном перемещении. Если
соприкасающиеся тела неподвижны друг
относительно друга, говорят о трении
покоя, если
же происходит относительное перемещение
этих тел, то в зависимости от характера
их относительного движения говорят о трении
скольжения, качения или верчения.
Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверхностей трение обусловлено силами межмолекулярного притяжения.
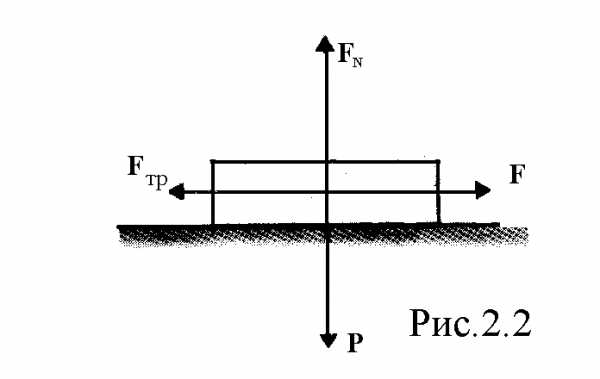
Рассмотрим
лежащее на плоскости тело (рис. 2.2), к
которому приложена горизонтальная сила  .
Тело придет в движение лишь тогда,
когда приложенная сила
.
Тело придет в движение лишь тогда,
когда приложенная сила будет больше силы трения
будет больше силы трения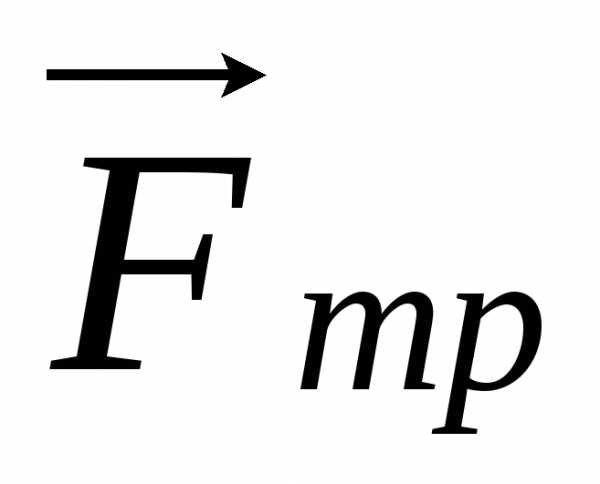 .
Французские физики Г. Амонтон и Ш.
Кулон опытным путем установили следующий
закон: сила трения скольженияFтр пропорциональна силе FN нормального давления, с которой одно
тело действует на другое:
.
Французские физики Г. Амонтон и Ш.
Кулон опытным путем установили следующий
закон: сила трения скольженияFтр пропорциональна силе FN нормального давления, с которой одно
тело действует на другое:
Fтр= μ FN , (2.11)
где μ – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.
Для гладких поверхностей определенную роль играет межмолекулярное притяжение. В этом случае закон трения скольжения имеет вид
Fтр = μист(FN +Sp0),
где p0– добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S – площадь контакта между телами; μист – истинный коэффициент трения скольжения.
Трение играет большую роль в природе и технике. Благодаря трению движется транспорт, удерживается забитый в стену гвоздь и т. д.
В некоторых случаях силы трения оказывают вредное действие, и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно меньшим внутренним трением жидкости.
Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники и т.д.).
б) Упругие силы. Под действием внешних сил возникают деформации (т. е. изменения размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, которое называется пределом упругости. При превышении этого предела деформация становится пластической. В этом случае после устранения внешних сил первоначальные форма и размеры тела полностью не восстанавливаются. В дальнейшем мы будем рассматривать только упругие деформации.
В деформированном
теле возникают упругие силы, которые
уравновешивают внешние силы, вызвавшие
деформацию. Поясним это на примере
деформации пружины. Под действием
внешней силы 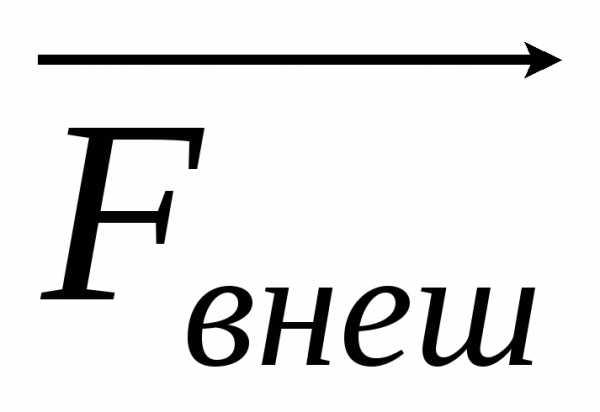 пружина
получает удлинение х,
в результате чего в ней возникает упругая
сила
пружина
получает удлинение х,
в результате чего в ней возникает упругая
сила  ,
уравновешивающая силу
,
уравновешивающая силу 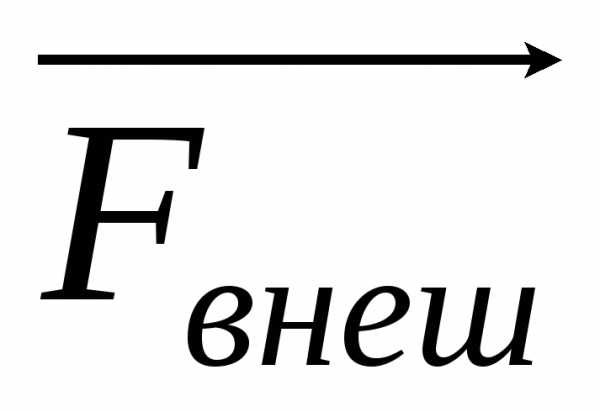 .
.
Упругие силы
возникают во всей деформированной
пружине. Любая часть пружины действует
на другую часть с силой, равной  .
.
Установленный экспериментально закон Гука утверждает, что при упругой деформации удлинение пружины пропорционально внешней силе. Аналитически эту закономерность принято записывать следующим образом:
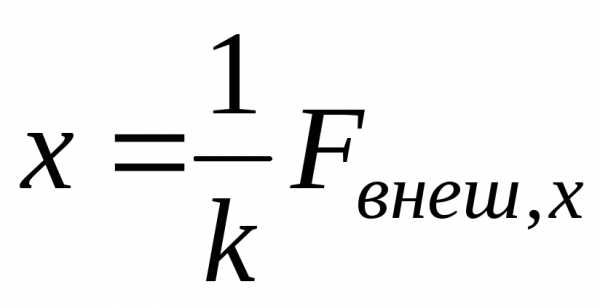 .
.
Величина k называется жесткостью пружины. Из этого выражения следует, что чем больше k, тем меньшее удлинение получает пружина под действием данной силы.
Упругая сила отличается от внешней только знаком. Поэтому Fупр,x = – Fвнеш,x и, следовательно,
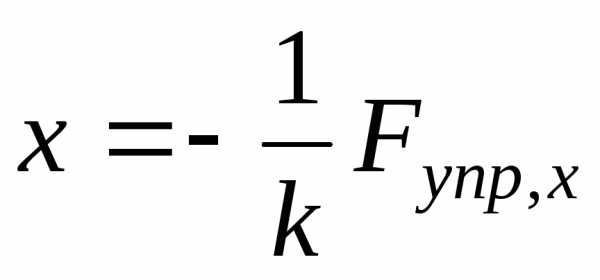 .
.
Опустим для краткости индекс «упр» и напишем это соотношение в виде Fx = – kx , (2.12)
где Fx – проекция упругой силы на ось х, k – жесткость пружины, х – удлинение пружины.
в) Силы тяжести и всемирного тяготения. И. Ньютон, изучая движение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m1 и m2) и обратно пропорциональная квадрату расстояния между ними (r2):
F = G m1m2 /r2. (2.13)
Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной.
Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Если же размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать силы притяжения между всеми попарно взятыми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей.
На любое тело, расположенное вблизи Земли, действует сила тяготения F, под влиянием которой, согласно второму закону Ньютона, тело начнет двигаться с ускорением свободного падения g. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой m действует сила
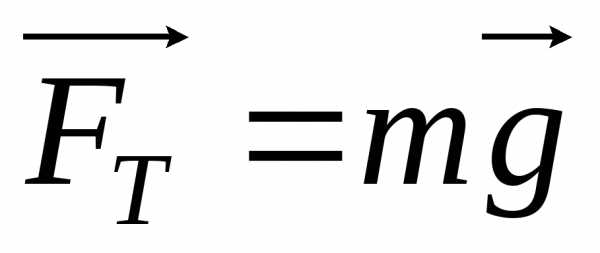 ,
(2.14)
,
(2.14)
называемая силой тяжести.
Согласно фундаментальному физическому закону – обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел.
Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила гравитационного тяготения равны между собой:
FТ = mg = G mM/R2, (2.15)
где М – масса Земли; R – расстояние между телом и центром Земли. Эта формула дана для случая, когда тело находилось вблизи поверхности Земли.
Если тело расположено на высоте h от поверхности Земли, R0 – радиус Земли, тогда
FТ = G mM/(R0 + h)2, (2.16)
т. е. сила тяжести с удалением от поверхности Земли уменьшается.
В физике
применяется также понятие веса тела. Весом тела 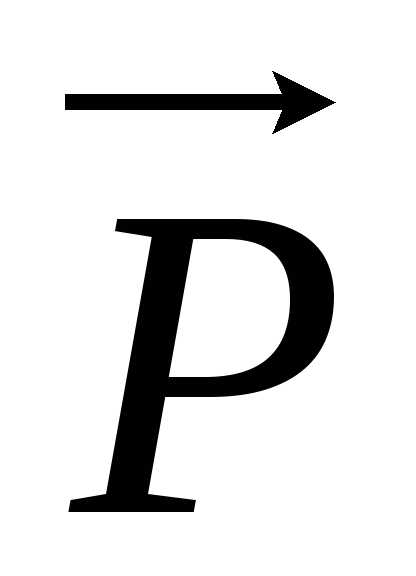 называют силу, с которой тело вследствие
тяготения к Земле действует на опору
(или подвес), удерживающую тело от
свободного падения. Вес тела проявляется
только в том случае, если тело движется
с ускорением, отличным от
называют силу, с которой тело вследствие
тяготения к Земле действует на опору
(или подвес), удерживающую тело от
свободного падения. Вес тела проявляется
только в том случае, если тело движется
с ускорением, отличным от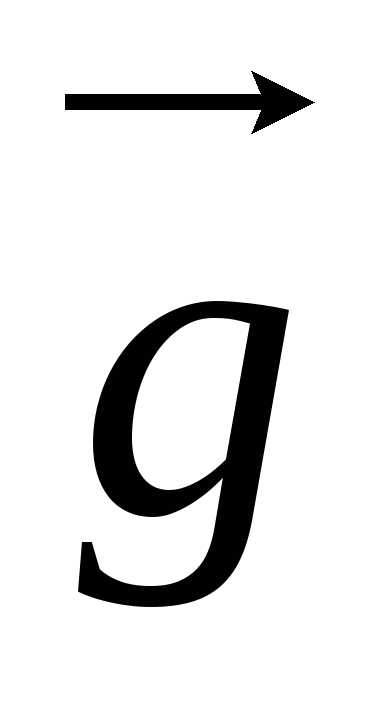 , т. е. когда на тело кроме силы тяжести
действуют другие силы. Состояние
тела, при котором оно движется только
под действием силы тяжести, называется
состоянием невесомости.
, т. е. когда на тело кроме силы тяжести
действуют другие силы. Состояние
тела, при котором оно движется только
под действием силы тяжести, называется
состоянием невесомости.
Таким образом,
сила тяжести действует всегда, а вес
появляется только в том случае, когда
на тело кроме силы тяжести действуют
еще другие силы, вследствие чего тело
движется с ускорением  ,
отличным от
,
отличным от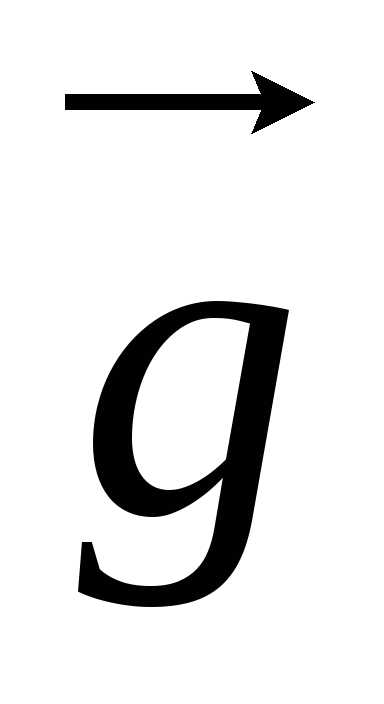 .
Если тело движется в поле тяготения
Земли с ускорением
.
Если тело движется в поле тяготения
Земли с ускорением ≠
≠ 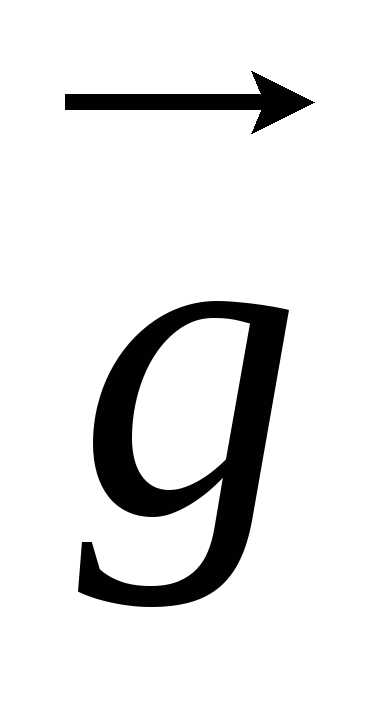 , то к этому
телу приложена дополнительная сила
, то к этому
телу приложена дополнительная сила  ,
удовлетворяющая условию
,
удовлетворяющая условию
.
Тогда вес тела , (2.17)
т. е. если тело
покоится или движется прямолинейно и
равномерно, то  = 0 и
= 0 и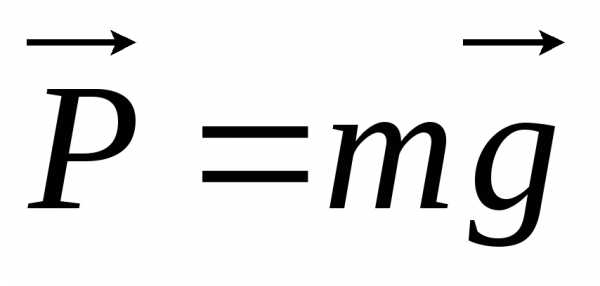 .
Если тело свободно движется в поле
тяготения по любой траектории и в
любом направлении, то
.
Если тело свободно движется в поле
тяготения по любой траектории и в
любом направлении, то =
= 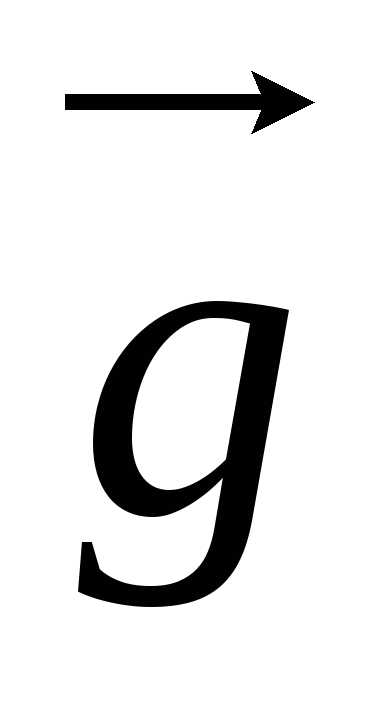 и
и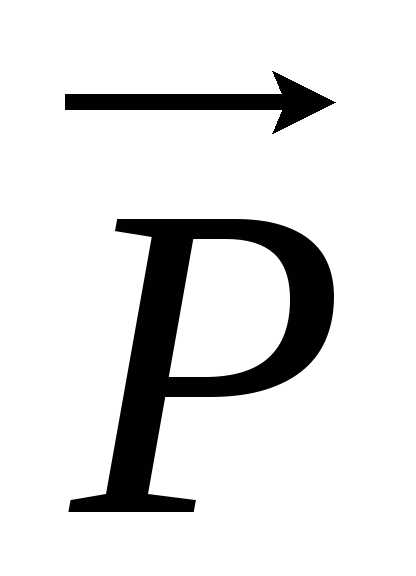 = 0, т. е. тело будет невесомым. Например,
невесомыми являются тела, находящиеся
в космических кораблях, свободно
движущихся в космосе.
= 0, т. е. тело будет невесомым. Например,
невесомыми являются тела, находящиеся
в космических кораблях, свободно
движущихся в космосе.
studfiles.net
2.3. Третий закон Ньютона
Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль прямой, соединяющей эти точки: F12= –F21, где F12 – сила, действующая на первую материальную точку со стороны второй; F21 – сила, действующая на вторую точку со стороны первой. Эти силы приложены к разным телам, всегда действуют парами и являются силами одной природы.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек: для системы материальных точек взаимодействие можно свести к силам парного взаимодействия между материальными точками.
Силы, подчиняющиеся трем законам Ньютона, называются ньютоновскими силами.
2.4.Закон сохранения импульса
Рассмотрим механическую систему – совокупность материальных точек, рассматриваемых как единое целое (m1, m2,…,mn – их массы, v1, v2,…,vn – их скорости). Силы взаимодействия между материальными точками системы называются внутренними (F1, F2,…Fn – равнодействующие внутренних сил, действующих на каждую из материальных точек). Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними (F1, F2,…Fn – равнодействующие внешних сил, действующих на каждую из материальных точек). Согласно третьему закону Ньютона, силы, действующие между материальными точками механической системы равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна нулю Fi = 0. Тогда второй закон Ньютона для механической системы имеет вид dp/dt=(d/dt)mivi=Fi, где p=mivi – импульс системы.
Механическая система, на которую не действуют внешние силы, называется замкнутой (изолированной). Следовательно, для изолированной (замкнутой) системы имеем выражение dp/dt=0 или p=mivi=const которое выражает закон сохранения импульса: импульс замкнутой (изолированной) системы не изменяется с течением времени. Закон сохранения импульса справедлив для любой замкнутой системы частиц, и он является фундаментальным законом природы. Закон сохранения импульса является следствием однородности пространства – при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются (иными словами, физические свойства и законы движения замкнутой системы не зависят от выбора положения начала координат инерциальной системы отсчета).
2.5.Силы трения
Из опыта известно, что тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил, с течением времени замедляет свое движение и останавливается. Это объясняется существованием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения могут быть различной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.
Различают внешнее (сухое) и внутреннее (жидкое, вязкое) трение. Внешнее трение возникает в плоскости касания двух тел при их относительном перемещении, и оно обусловлено шероховатостью соприкасающихся поверхностей (или обусловлено силами межмолекулярного взаимодействия, если поверхности очень гладкие). Если тела неподвижны, то говорят о трении покоя. Если тела движутся, то говорят о трении скольжения, качения или верчения.
Для силы скольжения имеет место экспериментальный закон Fтр = fN,
где N – сила нормального давления , f – коэффициент трения скольжения , зависящий от свойств соприкасающихся поверхностей. Для уменьшения трения скольжения используют смазку, которая заполняет неровности между поверхностями и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга – внешнее трение скольжения заменяется на значительно меньшее внутреннее трение жидкости. Другой способ уменьшения силы трения– замена трения скольжения на трение качения (шариковые и роликовые подшипники).
Для силы трения качения справедлив экспериментальный закон Fтр = fкN/r,
где r – радиус катящегося тела, fк – коэффициент трения качения.
studfiles.net
Законы Ньютона — Википедия
Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)[1][2]. В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.
Первый закон Ньютона
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.
Современная формулировка
В современной физике первый закон Ньютона принято формулировать в следующем виде[3]:
Историческая формулировка
Ньютон сформулировал первый закон механики так:
Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. |
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.
Видео по теме
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5][6][7].
Современная формулировка
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}где a→{\displaystyle {\vec {a}}} — ускорение материальной точки;
F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m} — масса материальной точки.
Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},} |
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени[8][9][10].
Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}} и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила[11][12].
Замечания
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}или
dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0}) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
Историческая формулировка
Исходная формулировка Ньютона:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. |
Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.
Третий закон Ньютона
Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}}, а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}}. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}}.
Современная формулировка
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.} |
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно[13].
Историческая формулировка
Ньютон дал следующую формулировку закона[1]:
Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. |
Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость[14].
Следствия законов Ньютона
Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.
Уравнения движения
Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.
Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
Закон сохранения импульса
Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю[15].
Закон сохранения механической энергии
Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной[16].
Законы Ньютона и силы инерции
Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.
Обычно речь идёт о силах инерции двух различных типов[13][17]. Сила первого типа (даламберова сила инерции[18]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции[18]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой[13][17]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются[19][13], их называют фиктивными[20], кажущимися[21] или псевдосилами[22].
Законы Ньютона в логике курса механики
Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.
Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.
Исторический очерк
Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем[23].
 Страница «Начал» Ньютона с аксиомами механики
Страница «Начал» Ньютона с аксиомами механикиОсновные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»[1]:
Оригинальный текст (лат.)
LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Русский перевод этих формулировок законов см. в предыдущих разделах.
Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)[24]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта[24]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).
В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).
Примечания
- ↑ 1 2 3 Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
- ↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
- ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
- ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
- ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
- ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
- ↑ 1 2 3 4 Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
- ↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
- ↑ 1 2 Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ 1 2 Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
- ↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
- ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
- ↑ 1 2 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
Литература
Ссылки
wikipedia.green
