Закон ома для неполной цепи – Закон ома для неполной цепи. Закон Ома. Для цепей и тока. Формулы. Применение

Закон Ома для полной цепи

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Ток, А	Напряжение, В	Сопротивление, Ом	Мощность, Вт
I	U	R	P

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^—iδ — комплексное сопротивление (импеданс),
• R = (R_a²+R_r²)^1/2 — полное сопротивление,
• R_r = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg R_r/R_a — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U₀sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

Закон Ома для полной цепи: от истории к формулам

Закон Ома для полной цепи – математическое выражение, описывающее зависимость между током и напряжением с учетом сопротивления источника. Так первоначально записана формула. Желающие посмотрят раздел про закон Ома для участка цепи.

Снова история

В истории были и будут белые пятна.

Катушка индуктивности

Отец катушки индуктивности доподлинно неизвестен. Причина — учёные беспрестанно обменивались опытом. На съездах академий наук шёл интенсивный процесс обсуждения различных точек зрения. Идея рождалась сообща. В трактате Георга Ома о математическом исследовании гальванических цепей касательно средств измерения нет сведений — непонятно, на что ориентировался муж науки. Стоит лишь посмотреть свод докладов того времени, становится понятно: сведения опущены по причине отсутствия выбора. На момент второго десятилетия XX века единственным индикатором силы тока считалась лишь магнитная стрелка. Череда событий:

1. 21 июля 1820 года Эрстед на латинском языке пишет про собственные опыты в области электромагнетизма. Оказывается, электрический ток может отклонять стрелку компаса. Эффект проявляется, когда контур замкнут – пишет учёный — и отсутствует, когда разомкнут. Сделано предположение, что угол отклонения зависит от «интенсивности движущегося электричества».
2. Чуть позднее в Женеве физики съехались посмотреть, как Ш. Г. Де ла Рив продемонстрирует необычное явление.
3. 4 сентября Араго на съезде академии наук поставил учёных в известность о новом открытии. Ампер, присутствующий на заседании в течение короткого времени сделал ряд открытий: соленоид с током ориентируется в магнитном поле земли, направление отклонения стрелки возможно заранее предсказать, проводники с током взаимодействуют между собой.
4. На указанном заседании академии (25 сентября), где высказался Ампер, физики Био и Савар доложили об открытии зависимости между током проводника и порождаемым им магнитным полем.

Учёный Швейгер

В сентябре 1820 года Швейггер представил на суд публики первый гальванометр, завершив подготовку материальной базы для исследований Георга Ома. Прибор учёный назвал мультипликатором за способность умножать эффект отдельных витков провода. К примеру, единственный экземпляр отклонял стрелку компаса на 30 градусов, а три – на 90. В конструкцию мультипликатора вклад внёс Поггендорф, использовавший для целей измерений катушку индуктивности из множества витков малого радиуса. Потом Зеебек при помощи нового средства открыл термоэлектрический эффект, использованный Георгом Омом (по совету Поггендорфа) при создании источника питания для собственной опытной установки.

В тесном контакте учёные за короткий промежуток времени совершили массу открытий. Причём каждое становилось известно интересующейся публике. Потому Георг Ом опустил в своём повествовании о математическом исследовании гальванических цепей такую малость, как сведения об экспериментальной установке. Примечательно, что уже электрический ток исследован, в науке появилось представление о напряжённости магнитного поля, но количественной зависимости между простейшими, как кажется сегодня, величинами не отмечалось. Никто понятия не имел о падении напряжения и сопротивлениях проводников.

Заслуга Георга Ома: количественно смог описать то, что сегодня применяется при любых электротехнических расчётах. Над упомянутой задачей бились титаны науки:

• Хемпфри Дэви;
• Беккерель;
• Барлоу;
• Мариани;
• Петров.

Исследователи, включая Риттера, Фуркруа, Тенара и Дэви, замечали, что проволока, будучи подключена к вольтову столбу, неизменно нагревалась. Возник вопрос: от чего зависит температура. От длины, материала, формы? Разнородные металлы опустошали источник энергии за разное время, в обиход стало пробиваться понятие электропроводности. После выхода в свет докладов Эрстеда параметр попытались охарактеризовать углом отклонения магнитной стрелки.

Путь Георга Ома к открытию закона для полной цепи

Странно, но имя Георга Ома сегодня известно более, нежели Майкла Фарадея, подарившего человечеству первый электродвигатель (если говорить точнее, истинный изобретатель пожелал остаться неизвестным, направив письмо, опубликованное позже в научном журнале). Без простого закона не возникли бы отрасли науки, техника выродилась в труд лопатой. Нет радио, телевидения и персональных компьютеров.

Изначально Георг Ом работал учеником слесаря, но отец хотел дать детям образование. Деньги на книги отряжались безотносительно к материальному благополучию. Георг Ом быстро усваивал науку, становясь талантливым математиком. Муж науки проявился как талантливый спортсмен и отменный плясун, не имевший равных на студенческих вечеринках.

Не успев закончить образование, отец закона для полной цепи пошёл учителем младших классов. Работал одновременно воспитателем. Быть учителем в швейцарском городе Готтштадте Георгу Ому нравилось: живописная природа и неплохой заработок, но истинный триумф ждал первооткрывателя закона для полной цепи сквозь невзгоды в будущем. В 1809 году проза жизни снова на пороге: к местному священнику возвращается сын – математик по образованию. Георгу предлагают оставить должность преподавателя.

Георг Ом

Более десяти лет Ом перебивается от одного места работы к другому, не находя удовлетворительного места для преподавания. Пока волею судьбы не оказывается приглашённым в иезуитскую школу Кельна. Преподавательская нагрузка невелика, зато в заведении присутствует обширное хранилище приборов, по большей части устаревших или сломанных. Любопытно, что Георг Ом не спешит бежать с прошением о материальной помощи к ректорам. Вместо этого, припомнив старые навыки слесаря, берётся мастерить собственными руками. С интересом в письмах отцу рассказывает о новых конструкциях, обычных и гидростатических, доводит до совершенства отцовский способ шлифовки янтаря для создания электрических источников.

Одновременно Георг Ом уделяет много времени конструированию прибора, называемого электрометром (измерение заряда на основании опытов Шарля Кулона). На сцене уже прогремели слухи о гальванометрах Швейггера, и Ом понимает, что в стройности науки далеко до совершенства. В 1821 году пишет отцу, что предчувствует некое открытие и внимательно следит за событиями в этой отрасли.

Изначально Ом брал вольтов элемент из меди и цинка, заправленный соляной кислотой, а крутильными весами измерял усилие, необходимое, чтобы привести стрелку к магнитному меридиану Земли, пока на компас действовал проводник с током. Провод Георг Ом ориентировал по меридиану, исключая погрешность. Вольтов столб разряжался сравнительно быстро, угол отклонения стрелки постепенно менялся. Ом видел, что источник в обычном качестве для экспериментальной установки не годится.

Образцы проволоки первоначально опускались в чашу с ртутью (имеющей сравнительно низкую проводимость) и тщательно зачищались учёным для лучшего контакта. Жидкая среда препятствовала окислению материала и одновременно ограничивала рост тока до разумных пределов. 5 образцов медной проволоки разной длины поочерёдно участвовали в эксперименте. Обозначив образцы латинскими буквами a, b, c, d, e новоиспечённый учёный Георг Ом находит свой первый закон в логарифмической форме:

Первый закон Ома

Где за х принимает длину проволоки в футах, U характеризует магнитное поле. Результаты не удовлетворяют учёного и через время он вносит в зависимость две константы:

U = m ln (1 + x/a) – первоначальная формулировка закона Ома для полной цепи.

От логарифмов к простому закону для полной цепи

Итак, если m равняется 0,525, при а = 2,9, полученная зависимость позволяет заранее предсказать результаты опыта. Параллельно учёный занимался исследованием проводимости различных металлов, в качестве эталона используя кусок меди длиною в 1 фут. Опытный образец укорачивался, пока отклонение магнитной стрелки не становилось тем же. Так исследованы свинец, золото, серебро, цинк, железо, латунь, платина и олово, но результаты часто не совпадали с ныне имеющимися на счету науки. Учёный видел расхождения и объяснял тем, что чистота образцов редко оказывалась стопроцентной.

Неудачи ждали и на пути определения зависимости отклонения стрелки от площади сечения. Не существовало инструмента, позволяющего точно провести оценку диаметра проволоки. Однако удалось установить, что проводимость явно зависит линейно от площади сечения и длины.

В первоначальном виде закон опубликован Журналом физики и химии, издаваемом Швейггером. На момент 1825 года Георг Ом неизвестен научным кругам, а формула, как видно, не совсем правильная и удобная. Учёный по тексту допустил оговорку, что исследование не окончено. Потрудился выпустить трактат (обсуждается в теме по закону Ома для участка цепи), где описал, на что опирается, подробно изложил умозаключения. Первое: сила тока одинакова на протяжении цепи. Это видно по степени отклонений магнитной стрелки. Заметим, что связь считалась, скорее, предположением, хотя не стоит забывать про закон Био-Савара (1820 год).

Одновременно учёный окончательно понял, что элемент Волластона (Вульстона) не годится. Это определялось по ослабевавшему накалу проволоки, но стоило лишь цепь разомкнуть и чуть выждать, как после повторного пуска температура достигала начального значения. Это явно говорило о нестабильности в первую и возобновляемости во вторую очередь такого источника. Одновременно схожей методикой пользовались Беккерель и Барлоу – оба опубликовали ошибочные выводы по зависимостям между параметрами проводника. Причём формулы выдвигались учёными различные, что явно указывало на необходимость продолжать поиск.

На помощь пришёл Поггендорф, который, разбирая напечатанную работу Ома, заявил, что в качестве источника лучше применить термо-ЭДС. Причём довёл сведения до Мартина – младшего брата Георга. Термопара из меди и висмута в составе установки находилась на штативе-треноге, снабжённой винтами для выставки в горизонт. Магнитная стрелка с крутильными весами служила крышкой прозрачному колпаку из стекла, защищающему рабочую часть от флуктуаций воздушного потока. Механик коллегии Маух помог Ому создать точную систему подстройки с градуированной шайбой, дабы точно засечь усилие, необходимое для возврата стрелки к магнитному меридиану Земли.

Даже стрелка компаса изготавливалась особой: из стали, с наконечниками из слоновой кости, единственный увенчан латунным указателем, нацеленным на шкалу. Насколько ответственно проведён эксперимент, настолько результат 1926 года оказался ближе к истине:

X = а/b + x.

Это закон Ома для полной цепи (I = U / R + r), где под Х понимается сила магнитного поля, прямо пропорциональная току I, а — термо-ЭДС U, x – длина проводника, прямо пропорциональная сопротивлению R, b – остальная часть цепи, подразумевающая сегодня внутреннее сопротивление r источника и контактов установки.

vashtehnik.ru

7. Закон Ома для электрической цепи.

Согласно этому законуcила тока I прямо пропорциональна напряжению U и обратно пропорциональна электрическому сопротивлению R цепи. Полное сопротивление замкнутой электрической цепи (рис. 9) можно представить в виде суммы сопротивления внешней цепи R (например, какого-либо приемника электрической энергии) и внутреннего сопротивления

R_o источника.

Поэтому сила тока : I = E/(R + R_o )

Чем больше э. д. с. Е источника и чем меньше сопротивление электрической цепи, тем больший ток проходит по этой цепи.

При применении Закона Ома к участку цепи, например между точками а и б (см. рис. 9) э. д. с. Е источника в формуле должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением

U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка. В этом случае закон Ома выражается формулой:

I = U/R

Из формулы следует, что напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка:

U = IR

Так как потенциал электрического поля в начале участка электрической цепи больше, чем в конце, разность потенциалов, или напряжение

U, приложенное к участку электрической цепи, часто называют падением напряжения на данном участке.

Исходя из закона Ома, если известны напряжение, приложенное к данному участку и сила тока на этом участке, можно найти сопротивление R этого участка

R = U/I

8. Использование резисторов для регулирования тока в электрической цепи.

Закон Ома показывает, что силу тока в электрической цепи можно изменять, включая в нее различные сопротивления. Электрический аппарат, предназначенный для включения в электрическую цепь с целью регулирования или ограничения проходящего по ней тока, называютрезистором. Резисторы бывают с постоянным или регулируемым сопротивлением (

реостатами).

Резисторы обычно изготовляют из проволоки или ленты, материалом для которых служат сплавы металлов, обладающие высоким удельным сопротивлением (константан, никелин, манганин, фехраль). Это дает возможность для изготовления резисторов применять проволоку наименьшей длины. Реостаты могут выполняться с плавным или ступенчатым изменением сопротивления.

Для регулирования тока при пуске тяговых двигателей постоянного тока применяют реостаты со ступенчатым изменением сопротивления (пусковые реостаты). Отдельные секции реостата в процессе пуска замыкаются накоротко контакторами (рис.11).

Пусковые реостаты электропоездов выполняют из фехралевой ленты 12, намотанной на фарфоровые изоляторы 13 (рис. 10,г).

Схемы включения реостатов. Реостат 2 (рис. 12) может быть включен последовательно в цепь между источником 1 и приемником 4 электрической энергии. В этом случае при изменении сопротивления реостата, т. е. при перемещении подвижного контакта 3, изменяется сила тока в приемнике. Этот ток проходит только по части сопротивления реостата. Однако реостат можно включать в цепь таким образом, чтобы ток проходил по всему его сопротивлению, а к приемнику ответвлялась только часть тока источника. В этом случае два крайних зажима 2 и 4 реостата (рис. 13) подключают к источнику 5, а один из этих зажимов, например 4, и подвижной контакт 3 реостата — к приемнику 1. Очевидно, что при таком включении к приемнику будет подаваться напряжение

U, равное падению напряжения между зажимом 4 и подвижным контактом 3 реостата. Следовательно, передвигая подвижной контакт реостата, можно изменять напряжение U, подводимое к приемнику, и силу тока в нем. Напряжение U представляет собой только часть напряжения U_и на зажимах источника.

Реостат, включенный по схеме рис. 13, называется делителем напряжения, или потенциометром.

studfiles.net

Закон Ома для полной цепи — Мегаобучалка

Если в результате прохождения постоянного тока в замкнутой электрической цепи происходит только нагревание проводников, то по закону сохранения энергии полная работа электрического тока в замкнутой цепи, равная работе сторонних сил источника тока, равна количеству теплоты, выделившейся на внешнем и внутреннем участках цепи:

(1)

По закону Джоуля – Ленца (см. ниже) количество теплоты, выделяющееся на проводнике сопротивлением R при силе тока I за время t равна:

Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внешний и внутренний участки которого имеют сопротивления R и r, равно:

(2)

Из выражений (1) и (2) получаем:

, но , следовательно,

Или

– закон Ома для полной цепи.

Сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.

 

Правило Кирхгофа.

При последовательном соединении нескольких источников тока полная эдс батареи равна алгебраической сумме эдс всех источников, а суммарное сопротивление равно сумме сопротивлений. При параллельном подключении n источников с одинаковыми эдс и внутренними сопротивлениями суммарная эдс равна эдс одного источника, а внутреннее сопротивление r_в=r/n. Если эдс источников различна, то для расчетов значения сил токов в различных участках цепи удобно пользоваться правилами Кирхгофа.

Первое правило Кирхгофа. Точка соединения нескольких проводников называется узлом. Алгебраическая сумма токов в узле равна нулю. Токи, идущие к узлу, будем считать положительными, от узла отрицательными. Второе правило Кирхгофа. Алгебраическая сумма падений напряжений на замкнутом контуре разветвленной цепи равна алгебраической сумме эдс.

Тепловое действие тока.Если через сопротивление R течет ток I, то кулоновские силы совершают положительную работу: A=qU=IUt, где q – количества электричества, протекшее через поперечное сечение проводника за промежуток времени t: q=It. При этом происходит выделение тепла Q. Очевидно, что Q=A, или Q=IUt=I²Rt=(U²/R)/t. (Закон Джоуля – Ленца).

 

правила, устанавливающие соотношения для токов и напряжений в разветвленных электрических цепях постоянного или квазистационарного тока. Сформулированы Г. Р. Кирхгофом в 1847. Первое К. п. вытекает из закона сохранения заряда и состоит в том, что алгебраическая сумма сил токов l_k, сходящихся в любой точке разветвления проводников (узле), равна нулю, т. е. ; здесь l – число токов, сходящихся в данном узле, причём токи, притекающие к узлу, считаются положительными, а токи, вытекающие из него,- отрицательными. Второе К. и. в любом замкнутом контуре, произвольно выделенном в сложной сети проводников алгебраическая сумма всех падений напряжений l_kR_k на отд. участках контура равна алгебраической сумме электродвижущих сил (эдс) E_k в этом контуре, т. е.

здесь m – число участков в замкнутом контуре (на рис. m = 3), I_kи R_k – сила тока и сопротивление участка номера k; при этом следует выбрать положительное направление токов и эдс, например, считать их положительными, если направление тока совпадает с направлением обхода контура по часовой стрелке, а ЭДС повышает потенциал в направлении этого обхода, и отрицательными – при противоположном направлении. Второе К. п. получается в результате применения Ома закона к различным участкам замкнутой цепи.

К. п. позволяют рассчитывать сложные электрические цепи, например, определять силу и направление тока в любой части разветвленной системы проводников, если известны сопротивления и эдс всех его участков. Для системы из n проводников, образующих r узлов, составляют n уравнений: r – 1 уравнение для узлов на основе первого К. п. (уравнение для последнего узла не является независимым, а вытекает из предыдущих) и n-(r-1) уравнений для независимых замкнутых контуров на основе второго К. п.; каждый из n проводников в эти последние уравнения должен войти хотя бы один раз. Т. к. при составлении уравнений нужно учитывать направления токов в проводниках, а они заранее не известны (и должны быть найдены из решения системы уравнений), то сначала эти направления задаются произвольно; если при решении для какого-нибудь тока получается отрицательное значение, то это означает, что его направление противоположно выбранному.

 

11. Мощность тока. Закон Джоуля-Ленца.
Почему выделяется тепло.

Мощность тока

Это работа, совершаемая за единицу времени и равная P=A/t=IU=I²R=U²/R. Полная мощность P₀, развиваемая источником, идет на выделение тепла во внешнем и внутреннем сопротивлениях и равна P₀=I²(R+r)=IE=E²(R+r). Мощность, выделяемая во внешнем сопротивлении, называется полезной мощностью и равна P_полез= E²R/(R+r)². Мощность, выделяемая во внутреннем сопротивлении, использована быть не может и называется теряемой мощностью Р_тер=I²r= E² r /(R+r)². Ток в электролитах. В электролитах (растворы солей, кислот, щелочей и расплавы солей ) имеются положительные и отрицательные ионы. В растворе устанавливается динамическое равновесие между процессами диссоциации и рекомбинации ионов. Под действием электрического поля ионы приобретают направленное движение – положительные ионы (катионы) движутся к катоду, отрицательные (анионы) – к аноду. При электролизе в растворах солей масса катода увеличивается, так как на катоде осаждаются положительные ионы. Например, если электролитом является раствор медного купороса, и мы берем медные электроды, то масса катода со временем увеличивается. Электролизом называется явление выделения вещества на электродах при прохождении через электролит электрического тока. Для электролиза справедливы два закона Фарадея: 1. Масса вещества, выделившегося при электролизе, прямо пропорциональна протекшему через электролит количеству электричества (заряду): m=kq=kIt, где k – электрохимический эквивалент данного вещества. Физический смысл электрохимического эквивалента состоит в следующем: k численно равен количеству вещества, выделившемуся при прохождении через электролит заряда [k] кг/Кл. 2. Второй закон Фарадея устанавливает связь между электрохимическим и химическим эквивалентом данного вещества: k=x/F, где х – химический эквивалент вещества, равный отношению атомной массы вещества А к его валентности n: x=A/n, F – постоянная Фарадея, не зависящая от свойств электролита, F=9,65*10⁴ Кл/моль. Объединив два закона получим объединенный закон Фарадея m=(1/F)(A/n)It, т.е. масса выделившегося вещества прямо пропорциональна атомной массе, силе тока, и времени и обратно пропорциональна валентности вещества. Если выделившаяся масса вещества численно равна его химическому эквиваленту, то постоянная Фарадея численно равна заряжу, который должен пройти через электролит, чтобы на электроде выделилась масса вещества, численно равная его химическому эквиваленту.

 

megaobuchalka.ru

Закон Ома для полной цепи

Закон Ома для полной цепи невозможно себе представить без такого параметра как  ЭДС.

Помню как-то на уроке физики в 8 классе препод спросил:

 — Что написано на пальчиковой батарейке?

 — Напряжение батарейки, — хором ответили мы.

 — Побрейтесь! Это ЭДС!

— !?

После этих гордых слов учитель начал вбивать нам свет истины в наши еще тупые тогда головы. Он ставил какие-то опыты, зажигал лампочки, писал что-то на доске… Но я все равно ничего не понял, потому что весь урок играл с товарищем по парте в морской бой ;-). Только спустя годы, прочитав советский словарь радиолюбителя, наконец-то до меня дошло, что ничего сложного в этом нет. И если закон Ома для участка цепи знают почти все, то сложности возникают именно по закону Ома для полной цепи. Но оказывается, все до боли просто!

Закон Ома для полной цепи на практике

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два проводка: красный на плюс, черный на минус

Наш акум готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

Первым делом давайте замеряем напряжение на клеммах акума

12,09 вольт. Вполне нормально, так как наш акум выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС нашего акума.

 

Подключаем  галогенку к акуму и снова замерям напряжение:

Видели да? Напряжение на акуме просело до 11,79 Вольт!

А давайте замеряем, сколько кушает наша лампа в Амперах. Для этого составляем вот такую схемку:

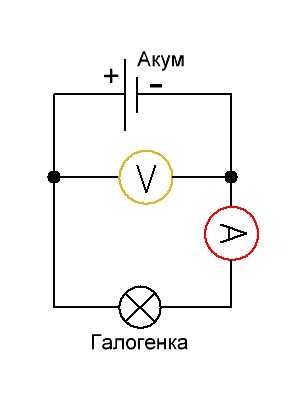
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

 

Давайте вместо галогенки поставим простую лампочку накаливания на 12 Вольт от поворотника мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на акуме. Вместо акума может быть простая батарейка полутора Вольт или какая-нибудь другая батарейка или аккумулятор. Суть от этого не меняется.

Закон Ома для полной цепи в теории

Источник ЭДС на схеме выглядит вот так:

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток, а точнее напряжение. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогеновых ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

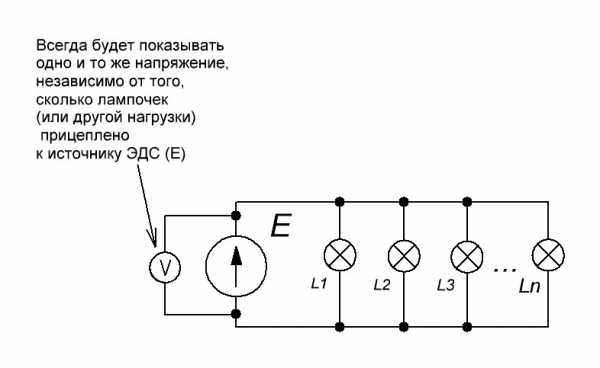
Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем акуме был идеальный источник ЭДС, тогда бы напряжение на клеммах акума никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока жрет нагрузка. Что-то здесь не так. Но почему так происходит? Этот вопрос задавал себе и немецкий физик Георг Ом и все-таки наконец-то он нашел объяснение этому феномену.

Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС акуммулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «. Выглядит все это в акуме примерно вот так:

Цепляем лампочку

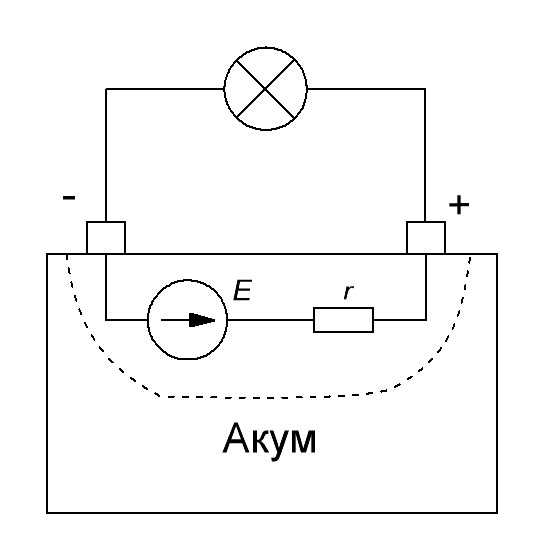
Итак, что у нас получается в чистом виде?

Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

 

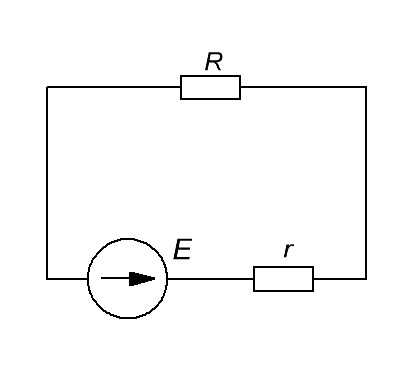
Итак, что имеем? Идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью  делитель напряжения            . Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом резисторе.

Это означает, что на каждом сопротивлении падает какое-то напряжение:

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r.

Теперь вспоминаем статью Делитель тока. Кто не помнит, напомню. Сила тока, протекающая  через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее

Последнее выражение носит название закона Ома для полной цепи. Из этого выражения мы можем найти внутреннее сопротивление акума «r».

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы цепанули нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

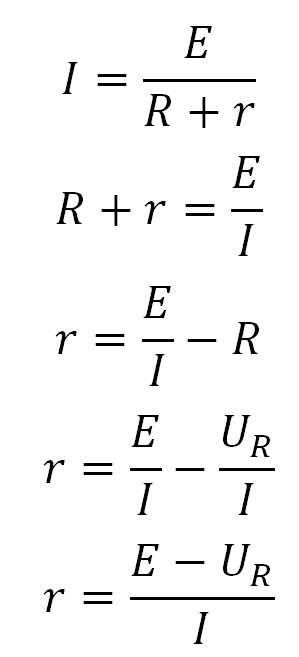
Получилось r=0,069 Ом

Резюме

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы. Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень жестко просядет напряжение. Это можно увидеть, если замкнуть клеммы акума толстым медным проводом и замерять в это время напряжение на клеммах)). Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник напряжения.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осцилл имеют ну очень большое сопротивление между своими щупами.

www.ruselectronic.com

Закон Ома для замкнутой цепи

Закон Ома для замкнутой цепи показывает – значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.

Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.

Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.

Формула закона Ома для замкнутой цепи записывается в следующем виде:

где:

• I [А] – сила тока в цепи,
• ε [В] – ЭДС источника напряжения,
• R [Ом] – сопротивление всех внешних элементов цепи,
• r [Ом] – внутреннее сопротивление источника напряжения

Физический смысл закона

Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.

Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.

Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.

Примеры задач на применение закона Ома для замкнутой цепи

К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.

Дано:	Решение:
ε = 10 В r = 1 Ом R = 4 Ом	Запишем закон Ома для замкнутой цепи – I=ε/(R+r) . Падение напряжения на зажимах источника найдем по формуле U=ε-Ir=εR/(R+r). Подставим заданные значения и вычислим I=(10 В)/((4+1)Ом)=2 А, U=(10 В∙4Ом)/(4+1)Ом=8 В./li> Ответ: 2 А, 8 В.

При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.

Дано:

Решение:

R1 = 20 Ом R2 = 10 Ом I1 = 1 A I2 = 1.5 A

Запишем закон Ома для замкнутой цепи – I=ε/(R+r) . Отсюда для каждого сопротивления получим ε=I_1 R_1+I_1 r, ε=I_2 R_2+I_2 r. . Приравняем правые части уравнений и найдем внутреннее сопротивление r=(I_1 R_1-I_2 R_2)/(I_2-I_1 ). Подставим полученное значение в закон Ома ε=(I_1 I_2 (R_2-R_1))/(I_2-I_1 ). Произведем вычисления r=(1А∙20 Ом-1,5А∙10Ом)/(1,5-1)А=10 Ом, ε=(1А∙1,5А(20-10)Ом)/((1,5-1)А)=30 В. Ответ: 30 В, 10 Ом.

zakon-oma.ru