ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Стр 1 из 2Следующая ⇒
Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.
Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.
Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтомузакон Ома для участка цепи
I = U/R.
Магический треугольник
Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
Как использовать треугольник Ома: закрываем искомую величину – два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.
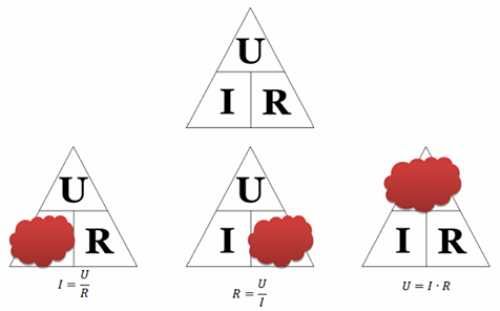
Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:
ампер = вольт/ом
Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.
Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.
Рис 1. Применение закона Ома для участка цепи
Приведем пример расчета тока по закону Ома. Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.
Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения
U = IR
Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению. Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.
Напряжение на участке цепи часто называют падением напряжения
Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.
Умножив I = 0,005 А на R —10000 Ом, получим напряжение,равное 50 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В
В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.
По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.
Закон Ома для полной цепи (DC)
Рассмотрим Закон Ома (Ohm’s law) для полной электрической цепи постоянного тока. Здесь нас прежде всего интересует его практическое отношение к постоянному току (direct current). Различают две формулировки Закона Ома, одна для участка цепи, а другая для полной цепи. В последней учитывается источник тока, точнее его внутреннее сопротивление.
Простейшая электрическая цепь постоянного тока состоит из источника тока и одной единственной резистивной нагрузки, а попросту из — активного сопротивления.

Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.
Чтобы выразить закон Ома математически наиболее просто, считают, что
Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтомузакон Ома для участка цепи записывается следующей формулой:
I = U/R.
Магический треугольник
Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
Как использовать треугольник Ома: закрываем искомую величину – два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.

Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:
Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.
Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.
Рис 1. Применение закона Ома для участка цепи
Приведем пример расчета тока по закону Ома. Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.
Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения
U = IR
Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению. Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.
Напряжение на участке цепи часто называют падением напряжения. Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны.
Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.
Умножив I = 0,005 А на R —10000 Ом, получим напряжение,равное 50 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В
В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.
По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.
Рекомендуемые страницы:
lektsia.com
Закон Ома
Оглавление1 Краткие теоретические сведения 3
1.1 Закон Ома 3
1.2 Обобщенный закон Ома 4
1.3 Взаимные преобразования звезды и треугольника сопротивлений 4
1.4 Законы Кирхгофа 5
1.4.1 Пример 1. 6
1.5 Метод контурных токов 8
1.5.1 Пример 2. 9
1.6 Метод узловых потенциалов 11
1.6.1 Пример 3 12
1.7 Метод эквивалентного генератора 14
1.7.1 Пример 3. 15
1.8 Потенциальная диаграмма 19
1.8.1 Пример 4. 19
2 Задание. 22
3 Библиографический список 35
Закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока без активных элементов (рис.1.1):
;
Рис.1.1
^
Обобщенный закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока, содержащем резистор и идеальный источник ЭДС (рис.1.2):
;
Формула справедлива для указанных на рис.1.2 положительных направлений падения напряжения на участке цепи (Uab), идеального источника ЭДС (Е) и положительного направления тока (I).
Рис.1.2
^
В сложных цепях встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным. К таким соединениям относятся трехлучевая звезда и треугольник сопротивлений (рис.1.3). Их взаимное эквивалентное преобразование во многих случаях позволяет упростить схему и свести ее к схеме смешанного (параллельного и последовательного) соединения сопротивлений. При этом необходимо определенным образом пересчитать сопротивления элементов звезды или треугольника.
Рис.1.3
Формулы эквивалентного преобразования треугольника сопротивлений трехлучевую звезду:
Формулы эквивалентного преобразования трехлучевой звезды сопротивлений в треугольник:
^
Режимы электрических цепей определяются первым и вторым законами Кирхгофа.
Первый закон Кирхгофа для цепи постоянного тока:
Алгебраическая сумма токов в узле равна 0.
;
Второй закон Кирхгофа для цепи постоянного тока:
Алгебраическая сумма падений напряжений на элементах контура равна алгебраической сумме ЭДС, действующих в этом же контуре.
Для составления системы уравнений на основании законов Кирхгофа необходимо:
Выбрать произвольно положительные направления искомых токов ветвей и обозначить их на схеме. Число токов должно быть равно числу ветвей схемы (В). Составить (Y – 1) – уравнений по первому закону Кирхгофа, где (Y) – число узлов схемы. Со знаком плюс учесть токи, втекающие в узел, а со знаком минус – вытекающие из узла.
Выбрать независимые контуры, число которых равно:
(НК) = (В) – (Y- 1)
Независимые контуры – контуры, отличающиеся друг от друга хотя бы одной новой ветвью.
Выбрать положительные направления обхода контуров (произвольно). Составить (В) – (Y – 1) уравнений по второму закону Кирхгофа для независимых контуров (НК), следуя правилу: если направление тока в ветви и направление обхода контура совпадают, напряжение на участке записать со знаком плюс. В противном случае – со знаком минус. Аналогично выбирают знак ЭДС.
Объединить уравнения, составленные по первому и второму законам Кирхгофа в систему алгебраических уравнений. Подставить численные значения и решить систему уравнений.
1.4.1 Пример 1.
| Дано: Е1=50 В Е2=400 В R1=50 Ом R2=20 Ом R3=50 Ом R4=80 Ом Определить токи в ветвях цепи (рис.1.4). |
| |
Рис. 1.4
Решение.
Произвольно зададим направления токов в ветвях цепи. В схеме 3 ветви (В = 3), два узла (Y = 2). По первому закону Кирхгофа можно составить одно независимое уравнение, (Y – 1) = (2 – 1) = 1:
Число независимых контуров:
(В) – (Y – 1) = 3 – (2 – 1) = 2
Выбираем направление обхода контуров по часовой стрелке, составляем два уравнения по второму закону Кирхгофа:
Составляем систему из уравнений, составленных по первому и второму законам Кирхгофа, подставляем численные значения:
Решив систему уравнений, получим:
skachate.ru
Обобщенный закон Ома для произвольного участка цепи — МегаЛекции
Структура электрической цепи.
Структура электрических цепей это соединения элементов определенным способом, и она не зависит от типа элементов. Поэтому структуру можно изучать по абстрактным графическим схемам цепи, на которых не отображается тип элементов. Такие схемы называют графами электрических цепей.
3. Граф и матрица электрической цепи:
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвьюграфа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Матрица (используются также другие названия этой матрицы: полная матрица инциденций, матрица соединений, структурная матрица) – это таблица, в которой число столбцов равно числу ветвей графа p, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. Элемент матрицы aij, расположенный на пересечении i-й строки и j-го столбца, может принимать значения +1, -1 и 0: aij = 1, если ветвь j инцидентна узлу i и направлена от этого узла; aij = -1, если ветвь j инцидентна узлу i и направлена к этому узлу; aij = 0, если ветвь j не инцидентна узлу i.
4. Законы Кирхгофа:
Cумма токов, подходящих к узловой точке электрической цепи, равна сумме токов, уходящих от этого узла.
В замкнутом контуре электрической цепи сумма всех ЭДС равна сумме падения напряжения в сопротивлениях того же контура.
E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn.
5. Эквивалентные преобразования последовательного параллельного и смешанного соединения потребителей:
При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.
R=R1+R2
При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви .Заменяя схемы параллельного соединения приемников лампы резисторами с сопротивлениями R1, R2, R3 При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R=R1*R2/(R1+R2)
Обобщенный закон Ома для произвольного участка цепи
IR = U12 = φ1 – φ2 + E
Где Е – ЭДС
Произведение силы тока на сопротивление участка цепи равно алгебраической сумме падения потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данным участке цепи.
8 Баланс мощностей:
В любой электрической цепи должен соблюдаться энергетический баланс – баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.
6. Эквивалентные преобразования соединения потребителей звездой и треугольником.
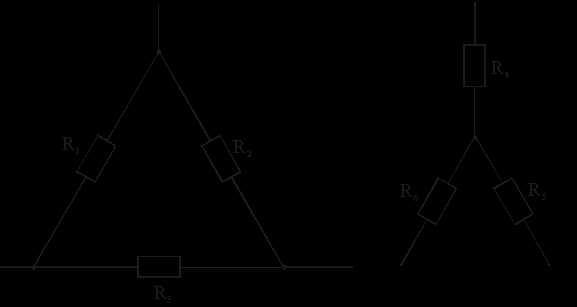
Звезда->Треугольник: Треугольник – > Звезда:
9. Расчет неразветвленных цепей.
Простейш неразветвленная цепь:
I=E/R
P=E*I
10. Расчет разветвленных цепей с одним источником.

RЭКВ = R1 + R2, 3 + R4
Uаб = R2, 3·I1
РИ = Е·I1
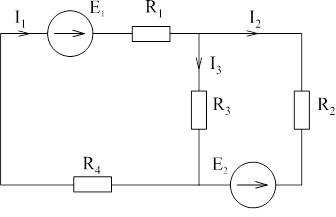
11. Метод уравнений Кирхгофа.
Рисунок для заданий 11-13:
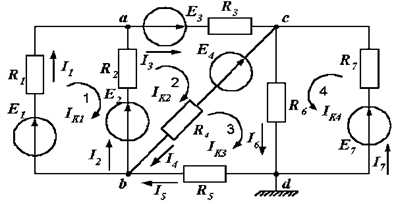
Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.
Эти системы дают достаточное количество уравнений для отыскания всех неизвестных токов.
12. Метод контурных токов.
Составляется системы уравнений по второму закону кирхгофа для контурных токов в каждом контуре:
После решения системы действительные токи ветвей определяются по найденным контурным:
13. Метод узловых потенциалов.
Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю.
Запишем для каждой ветви выражение закона Ома:
Подставляем эти токи в систему:
И получим n-1 уравнений (n-число узлов):

14. Метод наложения.
ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности. 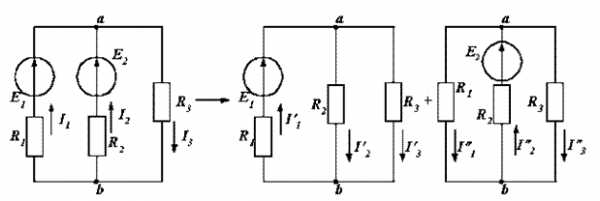

15. Метод эквивалентного источника напряжения.
Нужно рассчитать ток I3:
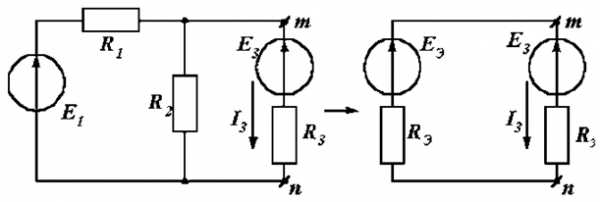
Р е ш е н и е.
а) Расчет режима холостого хода.
Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:
б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания:
Ik=E1/R1=75 (A)
Внутреннее сопротивление эквивалентного генератора:
Rэ=Ux/Ik 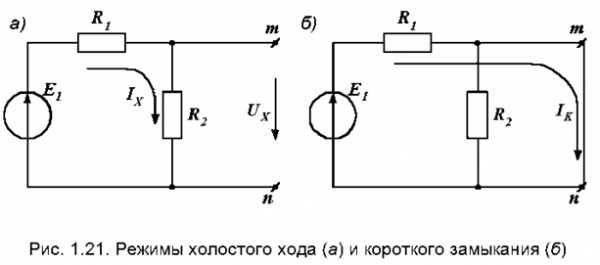
16. Цепи синусоидального тока. Основные характеристики гармонических сигналов. (3.1)
Период
Частота . (3.2)
Также существует понятие угловой (циклической) частоты:
. (3.3)
синусоидального тока и напряжения.
, (3.4)
где – мгновенное значение;
– амплитуда переменного сигнала – максимальная по модулю его величина;
– фаза гармонического сигнала – аргумент при синусе в каждый момент времени;
– начальная фаза – значение аргумента в начальный момент времени (t = 0). Фаза измеряется в радианах или градусах.
действующим значением тока:
. (3.8)
. (3.9)
Мгновенная мощность
Средняя мощность за период называется активной мощностью:
. (3.11)
17. Цепи синусоидального тока. Гармонический ток в сопротивлении.
Если напряжение u = Um sin(ωt + y) подвести к сопротивлению R, то через сопротивление пройдет гармонический ток
.
напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу,

18. Цепи синусоидального тока. Гармонический ток в индуктивности.
напряжение на емкости C синусоидально u = Umsin(wt+y).
Электродвижущая сила самоиндукции определяется по формуле
(1.3)
. Значит, напряжение на индуктивности
.

19. Цепи синусоидального тока. Гармонический ток в емкости.
ток i опережает приложенное напряжение и на угол π/2 
20. Цепи синусоидального тока. Последовательное соединение R, L, C.
Для мгновенных значений токов и напряжений выполняются I и II законы Кирхгофа.
При прохождении синусоидального тока через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по IIзакону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:
(3.21)
– цепь носит чисто активный характер
– цепь носит индуктивный характер, т.е. ;
– цепь носит емкостный характер, т.е. .
Полное сопротивление цепи
;
угол разности фаз
,
(3.24)
что удобно представлять с помощью треугольника сопротивлений (рис. 3.10).
Умножив левые и правые части выражений для сопротивлений (3.24) на действующее значение тока I, получим соответственно действующие значения напряжений на активном и реактивном сопротивлениях, которые называют активной и реактивной составляющими напряжения:
(3.25)
Тогда действующее значение суммарного напряжения можно определить как Для напряжений также можно построить прямоугольный треугольник напряжений.
21. Цепи синусоидального тока. Параллельное соединение R, L, C.
Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C приложено синусоидальное напряжение то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях
Активная проводимость цепи , всегда положительна.
Реактивная проводимость цепи , в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.
– угол разности фаз определяется по оси в направлении от напряжения к току и является острым или прямым .
– при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение.
– при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение.
– при резистивном характере цепи, т.е. при равенстве
22. …
23.Символический метод расчета. Законы Ома и Кирхгофа.
Закон Ома:
Пусть мгновенные значения напряжения и тока на зажимах произвольного пассивного двухполюсника определяются выражениями, комплексы действующих значений которых соответственно равны :
а их отношение определяет комплексное сопротивление двухполюсника:
Величина, обратная комплексному сопротивлению – комплексная проводимость:
Сопротивления z, R, x и проводимости y, G и B, входящие в два последних выражения, есть не что иное, как эквивалентные параметры двухполюсника.
24. Символический метод расчета. Последовательное соединение R, L, C.
Величины напряжений на отдельных элементах цепи:
Из треугольника oab по теореме Пифагора находим:
Вынося из под знака радикала, записываем последнее выражение в виде: U=I*z; где,z – полное сопротивление.
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = хL – xC.
Выражение U=Iz называется законом Ома для всей цепи. Оно может быть записано и так: I=U/z=Uy.
где, y– полная проводимость цепи, представляющая величину, обратную полному сопротивлению 1/z
Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений oab
25. Символический метод расчета. Параллельное соединение R, L, C.
Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов.
Требуется по известным G, ВL, ВC, U рассчитать токи
Подставив в уравнение первого закона Кирхгофа, получаем:
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
