Закона электромагнитной индукции фарадея формула – Закон электромагнитной индукции Фарадея — Википедия

Закон Фарадея для электромагнитной индукции и для электролиза

Для описания процессов в физике и химии есть целый ряд законов и соотношений, полученных экспериментальным и расчетным путем. Ни единого исследования нельзя провести без предварительной оценки процессов по теоретическим соотношениям. Законы Фарадея применяются и в физике, и в химии, а в этой статье мы постараемся кратко и понятно рассказать о всех знаменитых открытиях этого великого ученого.

История открытия

Закон Фарадея в электродинамике был открыт двумя ученными: Майклом Фарадеем и Джозефом Генри, но Фарадей опубликовал результаты своих работ раньше – в 1831 году.

В своих демонстрационных экспериментах в августе 1831 г. он использовал железный тор, на противоположные концы которого был намотан провод (по одному проводу на стороны). На концы одного первого провода он подал питание от гальванической батареи, а на выводы второго подключил гальванометр. Конструкция была похожа на современный трансформатор. Периодически включая и выключая напряжение на первом проводе, он наблюдал всплески на гальванометре.

Гальванометр — это высокочувствительный прибор для измерения силы токов малой величины.

Таким образом было изображено влияние магнитного поля, образовавшегося в результате протекания тока в первом проводе, на состояние второго проводника. Это воздействие передавалось от первого ко второму через сердечник – металлический тор. В результате исследований было обнаружено и влияние постоянного магнита, который двигается в катушке, на её обмотку.

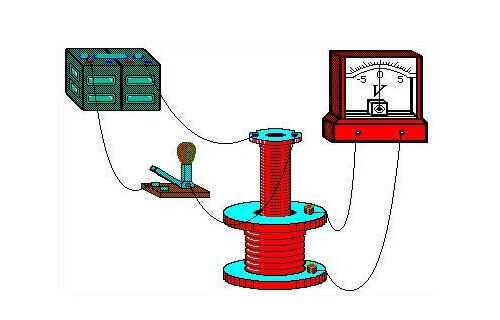
Тогда Фарадей объяснял явление электромагнитной индукции с точки зрения силовых линий. Еще одной была установка для генерирования постоянного тока: медный диск вращался вблизи магнита, а скользящий по нему провод был токосъёмником. Это изобретение так и называется — диск Фарадея.

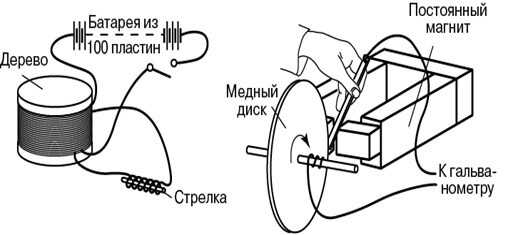
Ученные того периода не признали идеи Фарадея, но Максвелл взял исследования для основы своей магнитной теории. В 1836 г. Майкл Фарадей установил соотношения для электрохимических процессов, которые назвали Законами электролиза Фарадея. Первый описывает соотношения выделенной на электроде массы вещества и протекающего тока, а второй соотношения массы вещества в растворе и выделенного на электроде, для определенного количества электричества.

Электродинамика

Первые работы применяются в физике, конкретно в описании работы электрических машин и аппаратов (трансформаторов, двигателей и пр.). Закон Фарадея гласит:

Для контура индуцированная ЭДС прямо пропорциональна величине скорости магнитного потока, который перемещается через этот контур со знаком минус.

Это можно сказать простыми словами: чем быстрее магнитный поток движется через контур, тем больше на его выводах генерируется ЭДС.

Формула выглядит следующим образом:

Здесь dФ – магнитный поток, а dt – единица времени. Известно, что первая производная по времени – это скорость. Т.е скорость перемещения магнитного потока в данном конкретном случае. Кстати перемещаться может, как и источник магнитного поля (катушка с током – электромагнит, или постоянный магнит), так и контур.

Здесь же поток можно выразить по такой формуле:

B – магнитное поле, а dS – площадь поверхности.

Если рассматривать катушку с плотнонамотанными витками, при этом в количестве витков N, то закон Фарадея выглядит следующим образом:

Магнитный поток в формуле на один виток, измеряется в Веберах. Ток, протекающий в контуре, называется индукционным.

Электромагнитная индукция – явление протекания тока в замкнутом контуре под воздействием внешнего магнитного поля.

В формулах выше вы могли заметить знаки модуля, без них она имеет слегка иной вид, такой как было сказано в первой формулировке, со знаком минус.

Знак минус объясняет правило Ленца. Ток, возникающий в контуре, создает магнитное поле, оно направлено противоположно. Это является следствием закона сохранения энергии.

Направление индукционного тока можно определить по правилу правой руки или буравчика, мы его рассматривали на нашем сайте подробно.

Как уже было сказано, благодаря явлению электромагнитной индукции работают электрические машины трансформаторы, генераторы и двигатели. На иллюстрации показано протекание тока в обмотке якоря под воздействием магнитного поля статора. В случае с генератором, при вращении его ротора внешними силами в обмотках ротора возникает ЭДС, ток порождает магнитное поле направленное противоположно (тот самый знак минус в формуле). Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.

И наоборот — при протекании тока в роторе возникает поле, которое взаимодействует с полем статора и ротор начинает вращаться. При нагрузке на вал ток в статоре и в роторе повышается, при этом нужно обеспечить переключение обмоток, но это уже другая тема, связанная с устройством электрических машин.

В основе работы трансформатора источником движущегося магнитного потока является переменное магнитное поле, возникающее в следствие протекания в первичной обмотке переменного тока.

Если вы желаете более подробно изучить вопрос, рекомендуем просмотреть видео, на котором легко и доступно рассказывается Закон Фарадея для электромагнитной индукции:

Электролиз

Кроме исследований ЭДС и электромагнитной индукции ученный сделал большие открытия и в других дисциплинах, в том числе химии.

При протекании тока через электролит ионы (положительные и отрицательные) начинают устремляться к электродам. Отрицательные движутся к аноду, положительные к катоду. При этом на одном из электродов выделяется определенная масса вещества, которое содержится в электролите.

Фарадей проводил эксперименты, пропуская разный ток через электролит и измеряя массу вещества отложившегося на электродах, вывел закономерности.

m=k*Q

m – масса вещества, q – заряд, а k – зависит от состава электролита.

А заряд можно выразить через ток за промежуток времени:

I=q/t, тогда q = i*t

Теперь можно определить массу вещества, которое выделится, зная ток и время, которое он протекал. Это называется Первый закон электролиза Фарадея.

Второй закон:

Масса химического элемента, который осядет на электроде, прямо пропорциональна эквивалентной массе элемента (молярной массе разделенной на число, которое зависит от химической реакции, в которой участвует вещество).

С учетом вышесказанного эти законы объединяются в формулу:

m – масса вещества, которое выделилось в граммах, n – количество переносимых электронов в электродном процессе, F=986485 Кл/моль – число Фарадея, t – время в секундах, M молярная масса вещества г/моль.

В реальности же из-за разных причин, масса выделяемого вещества меньше чем расчетная (при расчетах с учетом протекающего тока). Отношение теоретической и реальной масс называют выходом по току:

B_т = 100% * m_расч/m_теор

Ну и напоследок рекомендуем просмотреть подробное объяснение закона Фарадея для электролиза:

Законы Фарадея внесли существенный вклад в развитие современной науки, благодаря его работам мы имеем электродвигатели и генераторы электроэнергии (а также работам его последователей). Работа ЭДС и явления электромагнитной индукции подарили нам большую часть современного электрооборудования, в том числе и громкоговорители и микрофоны, без которых невозможно прослушивание записей и голосовая связь. Процессы электролиза применяются в гальваническом методе покрытия материалов, что несет как декоративную ценность, так и практическую.

Похожие материалы:

samelectrik.ru

Закон электромагнитной индукции Фарадея

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра ОиОПД

Закон электромагнитной индукции Фарадея

Лабораторная работа № 2-8

г. Выкса

2006 г.

Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.

Даны сведения по закону индукции Фарадея, принципы действия генератора, трансформатора, методика и описание установки по измерению взаимной индукции.

Научный редактор А.А. Радионов

Цель работы: ознакомиться с законом электромагнитной индукции, принципом действия генератора, трансформатора, методикой измерения взаимной индуктивности.

Приборы и оборудование: две катушки (неподвижная и подвижная), звуковой генератор, электронный осциллограф, вольтметр.

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Пусть прямой проводник длинойl движется со скоростью в однородном магнитном поле с индукцией, как показано на рис.1. Вместе с ним движутся с той же скоростью все его заряды – положительные и отрицательные. Под действием сил Лоренца свободные заряды начинают перераспределяться, что ведет к появлению электрического поля. Силы Лоренца являютсясторонними силами. Электрическое поле, в свою очередь, начинает действовать на заряды силой . Когда силы, действующие на каждый заряд, уравновесятся, ЭДС индукции перестанет расти. Наведение ЭДС на проводнике, движущемся в магнитном поле, называетсяэлектромагнитной индукцией.

Работа сил Лоренца (сторонних сил) в расчете на единичный заряд равна ЭДС индукции:

(1)

Физический смысл знака минус выяснится ниже.

Для прямого проводника, движущегося прямолинейно и равномерно в однородном поле так, что его длина перпендикулярна векторами(см. рис.1).

(2)

– закон электромагнитной индукции в формулировке Фарадея.

Рассмотрим еще одно движение проводника в магнитном поле (рис. 2) – движение колесной пары 1—2 в однородном поле индукции (вид сверху). Так как, a , по формуле (2) можно написать:

,

где 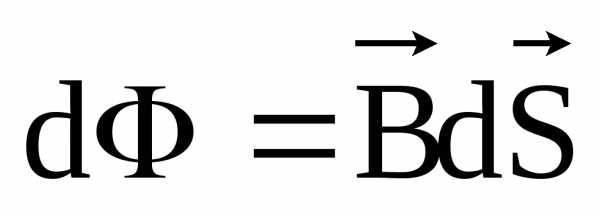– элементарное изменение магнитного потока через поверхность, ограниченную контуром определения ЭДС.

По определению, магнитным потоком через данную поверхность называется число линий индукции магнитного поля, проходящих через эту поверхность.

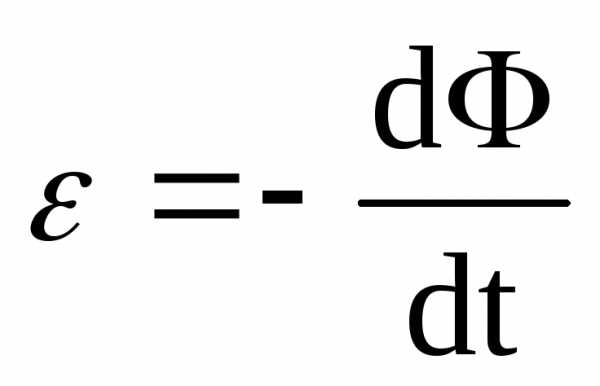(3)

– это математическая запись закона электромагнитной индукции в формулировке Максвелла.

ЭДС индукции, возникающая в контуре, равна скорости изменения магнитного потока через поверхность, опирающуюся на этот контур.

Движение проводника, в котором создается э. д. с. индукции, требует затраты механической энергии, которая по закону сохранения переходит в энергию электрического поля.

Пусть замкнутый проводник, сечение которого изображено на рис.3, движется в однородном магнитном поле. По закону электромагнитной индукции в нем возникает индукционный ток. Если бы индукционный ток был направлен на нас (возможны всего два направления, перпендикулярных плоскости чертежа), то сила АмпераF_a, действующая на проводник, была бы направлена вдоль скорости, проводник двигал бы сам себя и при этом индуцировался ток, т. е. был бы нарушен закон сохранения энергии. Остается лишь одна возможность: индукционный ток направлен в плоскость чертежа, сила Ампера препятствует движению, и необходимо совершить работу против этой силы, чтобы получить индукционный ток.

Мы получили правило Ленца – индукционный ток, возникающий в проводнике, имеет такое направление, что своим магнитным действием препятствует наводящему его движению. Это правило, говорящее как будто лишь о направлении индукционного тока, по существу является одним из наиболее общих выражений закона сохранения и превращения энергии. Его можно трактовать так: индукционный ток магнитным действием препятствует любой причине своего появления. Пусть какой-либо контур пронизывается возрастающим магнитным потоком (рис.4), т. е. 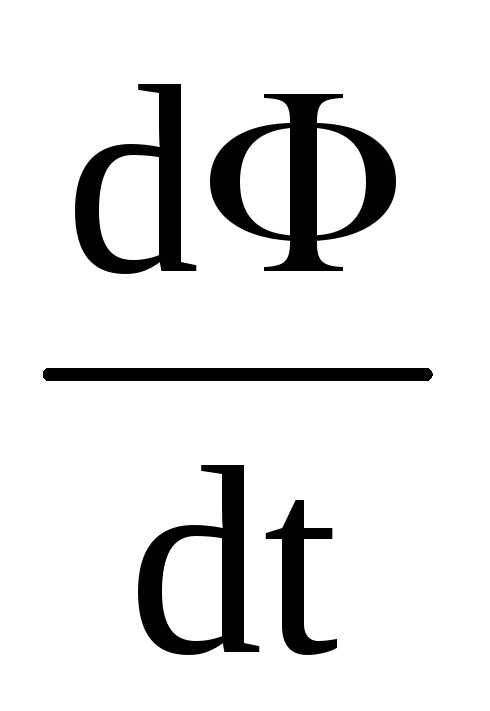>0. Индукционный ток, возникающий в контуре, по правилу Ленца имеет такое направление, при котором его магнитный поток мешает возрастанию наводящего магнитного потока. Индукционный ток, таким образом, связан с изменением магнитного потокаправилом левого винта.

ЭДС, возникающая в контуре, направлена так, что магнитный поток индукционного тока (если контур замкнут) противоположен по знаку изменению магнитного потока, наводящего ЭДС. Таков физический смысл знака минус, содержащегося во всех формулировках закона электромагнитной индукции.

Если в контуре сопротивлениемR изменяется магнитный поток на величину , то по данному контуру протекает определенный заряд ΔQ, который можно подсчитать:

.

Интегрируя почленно, получаем (без учета знака):

(4)

Рассмотрим контур, помещенный в магнитное; поле с индукцией(рис. 5). При всяком изменении магнитного потока Ф через площадьS поверхности, ограниченной контуром, в последнем возникает ЭДС индукции

, (5)

где – магнитный поток,- проекцияна нормальк площадке dS; N – число витков в контуре; 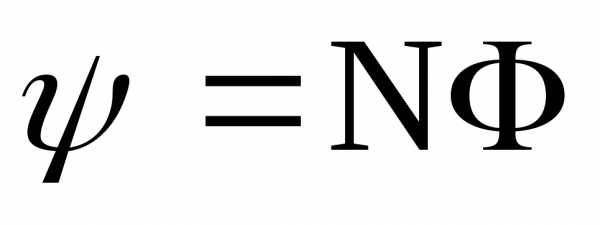потокосцепление. Соотношение (5) – закон электромагнитной индукции Фарадея. Знак минус в формуле соответствует правилу Ленца: индукционный ток всегда имеет такое направление, что он препятствует причине, его вызывающей.

Универсальность закона Фарадея в том, что ЭДС индукции не зависит от причины изменения магнитного потока, а они могут быть весьма различными. Приведем три примера. В электрогенераторе магнитный поток через витки катушки статора (рис.8) меняется вследствие того, что около катушки вращается электромагнит. В трансформаторе (рис. 9) напряжение первичной обмотки в соответствии с (5) изменяет поток, вследствие чего во вторичной обмотке возникает индукционный ток. Если разряжать конденсатор С после замыкания ключа К через сопротивление R и катушку индуктивности L, то поток уменьшается в катушке просто потому, что падает токI в катушке. Возникающую ЭДС ε=-LdI/dt называют ЭДС самоиндукции, L – индуктивностью катушки (рис. 6).

Рассмотрим два контура 1 и 2, расположенных на некотором расстоянии друг от друга (рис.7). Если по контуру 1 пропустить токI₁ то он создает поток магнитной индукции через контур 2:

(6)

Коэффициент пропорциональности М₂₁ называют коэффициентом взаимной индукции контуров (взаимной индуктивностью контуров). Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды.

При изменении силы тока в первом контуре магнитный поток сквозь второй контур изменяется. Следовательно, в нем наводится ЭДС взаимной индукции:

. (7)

Если поменять местами контуры 1 и 2 и повторить все предыдущие рассуждения, то получим:

. (8)

Можно показать, что коэффициенты взаимной индукции равны

.

ПРИНЦИП ДЕЙСТВИЯ ГЕНЕРАТОРА ПЕРЕМЕННОГО ТОКА

Закон индукции Фарадея лежит в основе электроэнергетики: на этом принципе действуют генераторы – источники электроснабжения промышленности и населения, трансформаторы. Простейший электрогенератор содержит вращающийся магнит (либо электромагнит) – ротор и неподвижную катушку статора (рис. 8). При вращении ротора в витках обмотки статора магнитный поток меняется по закону: , и возникает ЭДС индукции

,

обеспечивающая ток в нагрузке R.

ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА

Трансформатор (рис.9) содержит ферромагнитный сердечник, на котором две обмотки, первичная с числом витковn₁ и вторичная с n₂. К вторичной подключена нагрузка R, к первичной – источник напряжения U₁. В соответствии с законом Фарадея, U₁ вызывает рост магнитного потока Ф, (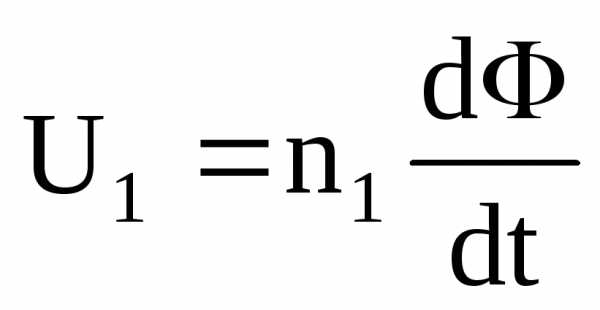). Сердечник, имеющий большую магнитную проницаемость (μ=400÷10000), выполняет две функции. Во-первых, он концентрирует магнитный поток так, что поток Ф через первичную и вторичную обмотки практически одинаков. Во-вторых, большое значение μ обеспечивает малый ток через первичную обмотку, когда нагрузка не подключена (ток холостого хода), т. е. снижает потери энергии при трансформации.

В соответствии с (5) на вторичной обмотке возникает напряжение 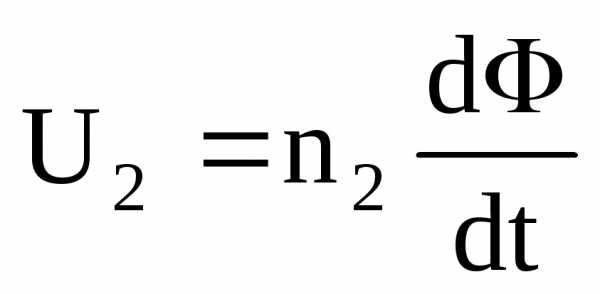, так что напряжение изменяется:

,

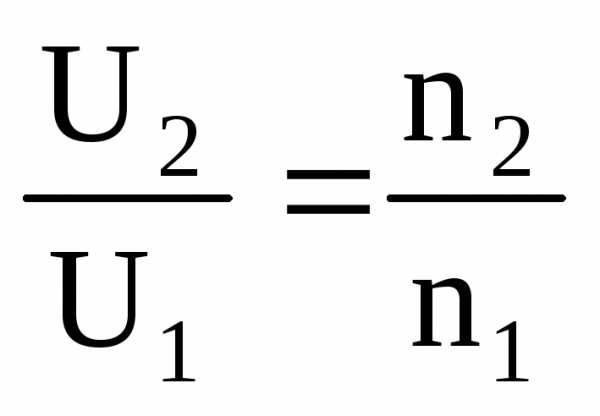где n₂/n₁ – коэффициент трансформации.

СОСТАВ УСТАНОВКИ

Вданной работе определяют взаимную индуктивность двух катушек (длинной катушки –L₁ и короткой катушки – L₂, которую надевают на катушку L₁ и могут перемещать вдоль ее оси). Схема установки представлена на рис.10. Питание одной из катушек (например L₁) осуществляется от генератора звуковой частоты, напряжение

(9)

с которого подается через резистор с сопротивленцем R. Вольтметр, расположенный на панели PQ, измеряет действующее напряжение.

Сопротивление выбирается таким, чтобы выполнялось неравенство

, (10)

где L₁ – индуктивность катушки L₁, R₁ – ее активное сопротивление. В этом случае силу тока, протекающего через катушку L₁, можно определить по формуле

. (11)

Переменный ток в катушке L₁ создает ЭДС индукции в катушке L₂:

. (12)

Для измерения ε₂ в данной работе используют осциллограф. Амплитуда ЭДС индукции

, (13)

где ν – частота звукового генератора. Из (13) имеем

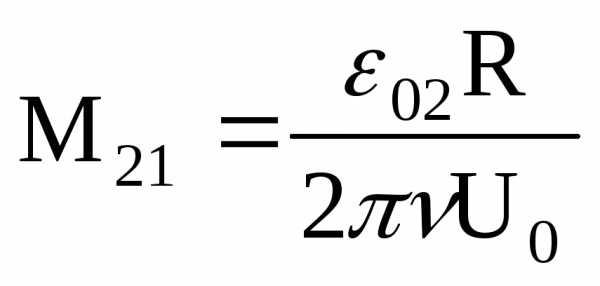. (14)

Если поменять местами катушки L₁ и L₂, то можно определить

(15)

ИЗМЕРЕНИЯ

Собрать установку, состоящую из звукового генератора, электронного осциллографа и двумя соосно расположенными катушками L₁ и L₂. Ознакомиться с работой звукового генератора и электронного осциллографа (см. описание), включить их в сеть 220 В, подготовить к работе.

УКАЗАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

1. Приборы питаются от сети 220 В. Включение в сеть приборов должно проводиться только в присутствие лаборанта или преподавателя.

2. Все корпусные клеммы приборов должны быть надежно заземлены (для заземления должен применяться провод без изоляции).

3. Запрещается работать в помещении одному.

Задание 1

Измерение взаимной индуктивности М₂₁ и М₁₂ и исследование их зависимости от взаимного расположения катушек

1. Напряжение сигнала со звукового генератора установите в диапазоне 1-4 В, а его частоту – в пределах 30-200 кГц.

2. Подайте напряжение на катушку L₁, а ЭДС с катушки L₂ на осциллограф.

3. Установите подвижную катушку L₁ в крайнее положение. Перемещая ее в противоположное крайнее положение, через каждый сантиметр запишите значение ЭДС магнитной индукции в цепи катушки L₂.

4. По формуле (14) рассчитайте М₂₁. Данные измерений и вычислений занесите в табл.1.

5. Поменяв местами катушки L₁ и L₂, повторите измерения по п.п. 1-4.

6. Постройте графики зависимости М₂₁ и М₁₂ как функции координаты z (z – расстояние между центрами катушек L₁ и L₂).

Таблица 1

z, см	ε02, В	М21 Гн	z, см	ε01, В	M21, Гн
UД=			ν=

Задание 2

Определение М21 для различных напряжений питания

1. Поставьте катушку L₁ в среднее положение относительно катушки L₂.

2. Установите частоту звукового генератора 10⁴ Гц.

3. Изменяя напряжение U_Д в цепи катушки L₁ снимите зависимость амплитуды ЭДС магнитной индукции от U_Д: ε₀₂=f(U_Д). Измерения провести в интервале 0-5 В через 0,5 В.

4. По формуле (14) рассчитайте M₂₁. Данные измерений и вычислений занесите в табл.2

Таблица 2

U0, В
ε02, В
М21, Гн
ν=		R=104 Ом

5. По данным табл. 2 найдите среднее значение М₂₁.

Задание 3

Определение М₂₁ для различных частот генератора

1. Поставьте катушку L₁ в среднее положение относительно катушки L₂.

2. Установите амплитуду напряжения звукового генератора 2 В.

3. Изменяя частоту генератора от 5 до 20 кГц (не менее 10 точек), снимите зависимость амплитуды ЭДС индукции ε₀₂ от частоты подаваемого напряжения.

4. По формуле (14) рассчитайте M₂₁. Данные измерений и вычислений занесите в табл.3.

Таблица 3

ν, Гц
ε02, В
М21, Гн
UД=		R=104 Ом

5. По данным табл. 3 найдите среднее значение М₂₁.

6. Для одного из полученных значений М₂₁ рассчитайте абсолютную и относительную погрешности ΔМ₂₁ и ΔМ₂₁/М₂₁.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте закон электромагнитной индукции (закон Фарадея) и правило Ленца.

2. В чем состоит явление электромагнитной индукции? Приведите примеры.

3. Принцип действия генератора переменного тока.

4. Принцип действия трансформатора.

5. В чем состоит явление взаимной индукции? От чего зависит взаимная индуктивность?

6. На замкнутом железном сердечнике с магнитной проницаемостью μ намотаны две катушки с числом витков n₁ и n₂. Вывести формулу для взаимной индуктивности, если длина сердечника l, a площадь поперечного сечения S.

12

studfiles.net

Закон электромагнитной индукции фарадея формулы — Экспресс Решение

Геометрическая оптика (3)

Физическая оптика (5)

Волновая оптика (1)

Электричество (39)

Атомная физика (15)

Ядерная физика (3)

Квадратный корень, рациональные переходы (2)

Квадратный трехчлен (1)

Координатный метод в стереометрии (1)

Логарифмы (1)

Логарифмы, рациональные переходы (1)

Модуль (1)

Модуль, рациональные переходы (1)

Планиметрия (1)

Прогрессии (1)

Производная функции (1)

Степени и корни (1)

Стереометрия (1)

Тригонометрия (1)

Формулы сокращенного умножения (1)

Закон индукции Фарадея

Закон индукции Фарадея — Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре , l который является границей поверхности S.

Закон Фарадея для электромагнитной индукции — Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур

В формуле мы использовали :

— Поток магнитной индукции

— Бесконечно малый элемент контура

— Бесконечно малый элемент вектора поверхности

xn--b1agsdjmeuf9e.xn--p1ai

Закон электромагнитной индукции Фарадея

История развития и опыты Фарадея

До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.

Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.

Рис. 1. Схема опыта Фарадея

На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.

Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).

Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.

Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.

Формула закона электромагнитной индукции Фарадея выглядит следующим образом:

Рис. 2. Формула закона электромагнитной индукции

И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.

Закон Фарадея-Максвелла

В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:

Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.

Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:

если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.

если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.

Рис. 3. Возникновение вихревого магнитного поля

Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.

Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.

obrazovaka.ru

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.

Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

источник – переменное магнитное поле;

обнаруживается по действию на заряд;

не является потенциальным;

линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитным потоком через площадь ? \( S \) ? контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ? \( B \) ?, площади поверхности ? \( S \) ?, пронизываемой данным потоком, и косинуса угла ? \( \alpha \) ? между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ? \( \Phi \) ?, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ? \( \alpha \) ? магнитный поток может быть положительным ( \( \alpha \) < 90°) или отрицательным ( \( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ? \( N \) ? витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ? \( R \) ?:

При движении проводника длиной ? \( l \) ? со скоростью ? \( v \) ? в постоянном однородном магнитном поле с индукцией ? \( \vec \) ? ЭДС электромагнитной индукции равна:

где ? \( \alpha \) ? – угол между векторами ? \( \vec \) ? и \( \vec \) .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ? \( \varepsilon_ \) ?, возникающая в катушке с индуктивностью ? \( L \) ?, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ? \( \Phi \) ? через контур из этого проводника пропорционален модулю индукции ? \( \vec \) ? магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ? \( L \) ? между силой тока ? \( I \) ? в контуре и магнитным потоком ? \( \Phi \) ?, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

закона электромагнитной индукции;

ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

fizi4ka.ru

Закон электромагнитной индукции Фарадея для начинающих

Что может быть лучше, чем вечером понедельника почитать про основы электродинамики. Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью. Времени занимает не много, а полезная информация останется в подсознании. Например, на экзамене, в условиях стресса, можно будет успешно извлечь из недр памяти закон Фарадея. Так как законов Фарадея несколько, уточним, что здесь мы говорим о законе индукции Фарадея.

Электродинамика – раздел физики, изучающий электромагнитное поле во всех его проявлениях.

Это и взаимодействие электрического и магнитного полей, электрический ток, электро-магнитное излучение, влияние поля на заряженные тела.

Здесь мы не ставим целью рассмотреть всю электродинамику. Упаси Боже! Рассмотрим лучше один из основных ее законов, который называется законом электромагнитной индукции Фарадея.

История и определение

Фарадей, параллельно с Генри, открыл явление электромагнитной индукции в 1831 году. Правда, успел опубликовать результаты раньше. Закон Фарадея повсеместно используется в технике, в электродвигателях, трансформаторах, генераторах и дросселях. В чем суть закона Фарадея для электромагнитной индукции, если говорить просто? А вот в чем!

При изменении магнитного потока через замкнутый проводящий контур, в контуре возникает электрический ток. То есть, если мы скрутим из проволоки рамку и поместим ее в изменяющееся магнитное поле (возьмем магнит, и будем крутить его вокруг рамки), по рамке потечет ток!

Этот ток Фарадей назвал индукционным, а само явление окрестил электромагнитной индукцией.

Электромагнитная индукция – возникновение в замкнутом контуре электрического тока при изменении магнитного потока, проходящего через контур.

Формулировка основного закона электродинамики – закона электромагнитной индукции Фарадея, выглядит и звучит следующим образом:

ЭДС, возникающая в контуре, пропорциональна скорости изменения магнитного потока Ф через контур.

А откуда в формуле минус, спросите Вы. Для объяснения знака минус в этой формуле есть специальное правило Ленца. Оно гласит, что знак минус, в данном случае, указывает на то, как направлена возникающая ЭДС. Дело в том, что создаваемое индукционным током магнитное поле направлено так, что препятствует изменению магнитного потока, который вызвал индукционный ток.

Для определения направления индукционного тока применяется знаменитое правило буравчика, или правило правой руки, оно же правило правого винта. Если ладонь правой руки расположить так, чтобы в неё входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока. Прямо у нас на сайте, вы также можете купить диплом по ПГС.

Примеры решения задач

Вот вроде бы и все. Значение закона Фарадея фундаментально, ведь на использовании данного закона построена основа почти всей электрической промышленности. Чтобы понимание пришло быстрее, рассмотрим пример решения задачи на закон Фарадея.

И помните, друзья! Если задача засела, как кость в горле, и нет больше сил ее терпеть — обратитесь к нашим авторам! Теперь вы знаете где заказать курсовую работу. Мы быстро предоставим подробное решение и разъясним все вопросы!

zaochnik.ru

Открытие Фарадея и Ленца: закон электромагнитной индукции — формула явления

В нашем мире все виды существующих сил, за исключением сил тяготения, представлены электромагнитными взаимодействиями. Во Вселенной, несмотря на удивительное разнообразие воздействий тел друг на друга, в любых веществах, живых организмах всегда встречается проявление электромагнитных сил. Как произошло открытие электромагнитной индукции (ЭИ), расскажем ниже.

Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.

Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в электричество.

Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию.

Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия.

Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность тока, возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита.

Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток. Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.

Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции.

Данный закон выражает формула:

Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна.

Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются:

магнит,

две проволочные катушки,

источник электроэнергии,

гальванометр.

Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.

Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки.

Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением.

Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества.

Другие законы Фарадея

На основе проведенных исследований были сформированы еще два одноименных закона:

Из всех существующих видов индукции огромное значение имеет обособленный вид данного явления – самоиндукция. Если мы возьмем катушку, которая имеет большое количество витков, то при замыкании цепи, лампочка загорается не сразу.

На этот процесс может уйти несколько секунд. Очень удивительный на первый взгляд факт. Чтобы понять, в чем здесь дело, необходимо разобраться, что же происходит в момент замыкания цепи. Замкнутая цепь словно «пробуждает» электроток, начинающий свое движение по виткам провода. Одновременно в пространстве вокруг нее мгновенно создается усиливающееся магнитное поле.

Катушечные витки оказываются пронизанными изменяющимся электромагнитным полем, концентрирующимся сердечником. Возбуждаемый же в витках катушки индукционный ток при нарастании магнитного поля (в момент замыкания цепи) противодействует основному. Мгновенное достижение им своего максимального значения в момент замыкания цепи невозможно, оно «растет» постепенно. Вот и объяснение, почему лампочка не вспыхивает сразу. Когда цепь размыкается, основной ток усиливается индукционным в результате явления самоиндукции, и лампочка ярко вспыхивает.

Направление тока самоиндукции определяет правило Ленца. Самоиндукция легко сравнима с инерцией в области механики, поскольку оба явления обладают схожими характеристиками. И действительно, в результате инерции под влиянием силы тело приобретает определенную скорость постепенно, а не сиюминутно. Не сразу – под действием самоиндукции — при включении батареи в цепь появляется и электричество. Продолжая сравнение со скоростью, заметим, он так же не способен мгновенно исчезнуть.

Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.

Специалисты знают, что металлические трансформаторные сердечники, якоря генераторов и электродвигателей никогда не бывают сплошными. При их изготовлении на отдельные тонкие листы, из которых они состоят, накладывается слой лака, изолирующий один лист от другого.

Нетрудно понять, какая сила заставляет человека создавать именно такое устройство. Под действием электромагнитной индукции в переменном магнитном поле сердечник пронизывают силовые линии вихревого электрополя.

Представим, что сердечник изготовлен из сплошного металла. Поскольку его электрическое сопротивление невелико, возникновение индукционного напряжения большой величины было бы вполне объяснимым. Сердечник бы в итоге разогревался, и немалая часть электрической энергии терялась бесполезно. Кроме того, возникла бы необходимость принятия специальных мер для охлаждения. А изолирующие слои не позволяют достигать больших величин.

Индукционные токи, присущие массивным проводникам, называются вихревыми не случайно – их линии замкнуты подобно силовым линиям электрополя, где они и возникают. Чаще всего вихревые токи применяются в работе индукционных металлургических печей для выплавки металлов. Взаимодействуя с породившим их магнитным полем, они иногда становятся причиной занимательных явлений.

Возьмем мощный электромагнит и поместим между вертикально расположенными его полюсами, к примеру, пятикопеечную монету. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды.

Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.

Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Передвижение монеты напоминает перемещение тела в вязкой среде. Почему такое происходит.

По правилу Ленца направления возникающих при передвижении монеты вихревых токов в неоднородном магнитном поле таковы, что поле магнита выталкивает монету вверх. Эту особенность используют для «успокоения» стрелки в измерительных приборах. Алюминиевая пластина, находящаяся между магнитными полюсами, прикрепляется к стрелке, и вихревые токи, возникающие в ней, способствуют быстрому затуханию колебаний.

Демонстрацию явления электромагнитной индукции поразительной красоты предложил профессор Московского университета В.К. Аркадьев. Возьмем свинцовую чашу, обладающую сверхпроводящей способностью, и попробуем уронить над ней магнит. Он не упадет, а будет словно «парить» над чашей. Объяснение здесь простое: равное нулю электрическое сопротивление сверхпроводника способствует возникновению в нем электричества большой величины, способных сохраняться продолжительное время и «удерживать» магнит над чашей. По правилу Ленца, направление магнитного поля их таково, что отталкивает магнит и не дает ему упасть.

Изучаем физику — закон электро-магнитной индукции

Электромагнитные силы – это силы, которые позволяют людям видеть окружающий мир и чаще других встречаются в природе, например, свет — тоже пример электромагнитных явлений. Жизнь человечества невозможно представить без данного явления.

expressreshenie.ru

Закон Фарадея: формула для электромагнитной индукции

Майкл Фарадей (1791-1867) родился в Англии и жил, можно сказать, для изучения физики и химии. Он считается основателем концепции об электромагнитном поле и автором закона электромагнитной индукции, а также первооткрывателем формулы электромагнитной индукции.

Данное направление физики дало старт к промышленному производству электричества. Подтолкнуло его к этому открытие, которое совершил Эрстед. В нем доказано, что при запуске тока через прямой передатчик вокруг этого передатчика возникает магнитное поле.

Фарадей задумался над обратным эффектом, где магнитное поле, в котором проводник в замкнутом состоянии, может продуцировать ток.

Опыты Фарадея на пути к открытию

Фарадей — один из самых значимых физиков в истории

На протяжении десяти лет он пытался доказать свою теорию. И в 1831 году Фарадей провел ряд удачных опытов, которые служили безупречным доказательством.

Фарадей разместил на основании из дерева две катушки, обозначим их катушкой А и катушкой Б.

Обмотка катушки Б была изолирована, располагалась между обмоткой катушки А.

Катушка А была подключена к гальванической батарее, а катушка Б к гальванометру, чтобы измерить движение токов.

В итоге сформировались две независимые цепи гальваническая батарея — Катушка А и Катушка Б — гальванометр.

Обмотки катушек ничем не были соединены между собой, существовало только магнитное поле продуцируемое катушкой А, которое охватывало катушку Б.

Как только замыкали катушку А, гальванометр показывал незначительный электрический импульс. В дальнейшем, при постоянном токе в катушке А, гальванометр не показывал никаких изменений в катушке Б.

Но как только цепь в катушке А размыкалась, гальванометр опять фиксировал импульс тока в катушке Б, который двигался в обратном направлении.

Данный опыт позволил Фарадею сделать выводы о том, что магнитное поле катушки А, которое меняется относительно времени, рождает электрический ток в катушке Б.

Появление тока в данных условиях определяется как индукция, поэтому ток считается индукционным.

Примечательно, при росте магнитного поля, в случае, когда цепь с катушкой А активна, электрический ток в катушке Б движется в одном направлении, а когда магнитное поле слабеет, во время отключения цепи с катушкой А, ток движется в противоположную сторону.

Возникновение электричества с помощью магнетизма Фарадей определил как явление электромагнитной индукции.

Чтобы убедиться в том, что источник возникновения тока — это переменное магнитное поле, Фарадей двигал катушки по отношению друг к другу, при этом ток в катушке А был постоянным, а за счет движения, Катушка Б была в переменном магнитном поле и индуцировала электрический ток.

Исходя из этого опыта он сделал вывод — с увеличением скорости движения катушки, увеличивалась сила индукционного тока.

Затем катушка А была заменена источником высокой остаточной магнитной индукцией — магнитом, и Фарадей подтвердил опыт со сближением и удалением Катушки Б, которая подключена к гальванометру.

Как и в предыдущем опыте, гальванометр показал ток, который двигался в одном направлении при сближении с магнитом и менял направление на противоположное при отдалении от магнита.

И вновь сила тока увеличивалась при увеличении скорости движения катушки.

После этих опытов Фарадей пришел к выводу, что на возникновение индукционного тока влияет изменение количества линий магнитного поля, через которое проходит катушка.

Иначе говоря, чем больше магнитных линий будет пройдено через катушку Б за короткий промежуток времени, тем выше сила индукционного тока. Число линий, которые проходят через ограниченную площадь проводника определяется как магнитный поток.

Чем выше индукция, тем больше линий магнитного потока, и если умножить их на площадь проводника, учитывая угол наклона к плоскости проводника, можно вычислить магнитный поток.

Формула электромагнитной индукции

Закон электромагнитной индукции дал старт разработкам генераторов

Зная все критерии опыта, можно определить что такое электромагнитная индукция.

Электромагнитная индукция — это появление электрического тока в замкнутом проводнике при изменении магнитного потока, который проходит через проводник.

Главное определение закона электродинамики Фарадей определил так:

Электродвижущая сила, которая возникла в проводнике, пропорциональна скорости изменения магнитного потока, проходящего через проводник.

ε = -dФ/ dt

ε — это электродвижущая сила

dФ — дифференциальная величина электромагнитного потока,

dt — дифференциальная величина времени прохождения потока через контур

Знак «-» в формуле появился после определения правила Ленца. Он выяснил, что индукционный поток всегда противодействует причине, которая его вызывает.

Формулу можно применять как в ситуации с неподвижным контуром, так и при движении проводников в магнитном поле.

Входящая в нее производная от магнитного потока по времени в общем случае включает в себя две части, первая часть определена переменой магнитной индукции во времени, а вторая – движением проводника по отношению к магнитному полю.

Закон электромагнитной индукции дал старт разработкам генераторов, которые устроены наподобие опытов Фарадея:

• ротор, который двигается;
• статор, находящийся в неизменном положении;
• возникшее между ними электромагнитное поле.

Через обмотку статор проходит электрический ток, который вырабатывает магнитное поле, это поле влияет на магнитное поле ротора, под действием этой силы раскручивается вал.

В этом видео вы увидите целый урок на тему закона Фарадея для электромагнитной индукции:

vyuchit.work

Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме

Задание: Найдите ЭДС индукции как функцию ${{\mathcal E}}_i$ от расстояния $x$ для квадратной рамки с током. Рамка имеет сторону $a$ и находится в одной плоскости с проводников с током силы $I$. Рамка движется поступательно с постоянной скоростью $v$. Направление движения указано на рис.1.

Рисунок 1.

Решение:

В качестве основания для решения задачи используем закон Фарадея:

\[{{\mathcal E}}_i=-\frac{dФ}{dt}\left(2.1\right).\]

Для того чтобы получить искомую функцию ${{\mathcal E}}_i(x)$, построим функцию $Ф(x)$. Магнитное поле, в котором находится рамка, создается бесконечным проводником с током, оно может быть представлено как:

\[B=\frac{{\mu }_0I}{2\pi r}\left(2.2\right),\]

где $r$ расстояние до точки, в которой рассматривается поле.

Выделим элемент площади $(dS)$ рамки, величина которого может быть выражена как:

\[dS=adr\left(2.3\right).\]

В таком случае, элементарный магнитный поток через элемент квадратной рамки, используя выражения (2.2), (2.3) и определение потока, учитывая, что $\overrightarrow{B}\bot \overrightarrow{S}$, можно записать как:

\[dФ=BdS=\frac{{\mu }_0I}{2\pi r}adr\left(2.4\right).\]

Вычислим полный поток, если $x\le r\le x+a$:

\[Ф=\int\limits^{x+a}_x{\frac{{\mu }_0I}{2\pi r}adr}=\frac{{\mu }_0Ia}{2\pi }ln\frac{x+a}{x}\left(2.5\right).\]

Используя закон Фарадея (2.1) и выражение для магнитного потока (2.5) найдем ЭДС индукции:

\[{{\mathcal E}}_i=-\frac{dФ}{dx}\cdot \frac{dx}{dt}=-\frac{{\mu }_0Ia}{2\pi }\cdot \frac{x}{x+a}\left(x^{-1}-\left(x+a\right)x^{-2}\right)\cdot v=-\frac{{\mu }_0Ia}{2\pi }\cdot \frac{x}{x+a}\left(\frac{x-x-a}{x^2}\right)\cdot v=\frac{{\mu }_0Ia^2v}{2\pi \left(x+a\right)x}.\]

Ответ: ${{\mathcal E}}_i$=$\frac{{\mu }_0Ia^2v}{2\pi \left(x+a\right)x}.$

spravochnick.ru

Реферат Закон электромагнитной индукции Фарадея

скачать

Реферат на тему:

План:

Введение

• 1 Закон Фарадея
  • 1.1 Векторная форма
  • 1.2 Потенциальная форма
• 2 История
Примечания

Введение

Не следует путать с вектором электрической индукции.

Не следует путать с вектором магнитной индукции.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Майклом Фарадеем в 1831 году. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

1. Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в системе СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

 — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

1.1. Векторная форма

В дифференциальной форме закон Фарадея можно записать в следующем виде:

(в системе СИ)

или

(в системе СГС).

В интегральной форме (эквивалентной):

(CИ)

или

(CГС)

Здесь  — напряжённость электрического поля,  — магнитная индукция,  — произвольная поверхность,  — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

• В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[1].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство продолжает соблюдаться, но ЭДС в левой части теперь не сводится к (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (т.е. порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

• Некоторые авторы^[2] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции итп к формуле в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[3]. В таком понимании закон Фарадея – это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.

1.2. Потенциальная форма

При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:

(в случае отсутствия безвихревого поля, т.е. тогда, когда электрическое поле порождается полностью только изменением магнитного, т.е. электромагнитной индукцией).

В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:

2. История

В 1820 г. Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 г. в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 г. наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, заключалась в том, что Фарадей изготовил кольцо из мягкого железа примерно 2 см шириной и 15 см диаметром и намотал много витков медной проволоки на каждой половине кольца. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.

Американский физик Джозеф Генри тоже успешно проводил опыты по индукции токов. Но пока Д. Генри собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции. То, что два учёных независимо друг от друга пришли к одному и тому же результату, не удивительно.

М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.

Примечания

1. Это уравнение Максвелла может быть переписано в эквивалентном виде
   (здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, т.к. производная теперь очевидно не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается “мгновенным”. В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
2. См. например [[1] – kvant.mirror1.mccme.ru/pdf/1998/03/kv0398lifshits.pdf].
3. Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, “правило” корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (т.е. совпадает их движение; в противном же случае правило может не работать (самый известный пример – униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), т.е. проявляется парадокс, что для “закона природы” недопустимо.

wreferat.baza-referat.ru

51.5. Закон электромагнитной индукции Фарадея.

51.5. Закон электромагнитной индукции Фарадея.

 Мы достаточно подробно рассмотрели три различных, на первый взгляд, варианта явления электромагнитной индукции, возникновения электрического тока в проводящем контуре под действием магнитного поля: при движении проводника в постоянном магнитном поле; при движении источника магнитного поля; при изменении во времени магнитного поля. Во всех этих случаях закон электромагнитной индукции одинаков:
 ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через контур, взятой с противоположным знаком

независимо от причин, приводящих к изменению этого потока.
 Уточним некоторые детали приведенной формулировки.
 Первое. Магнитный поток через контур может изменяться произвольным образом, то есть функция Ф(t) не обязана всегда быть линейной, а может быть любой. Если магнитный поток изменяется по линейному закону, то ЭДС индукции в контуре постоянна, в этом случае величина интервала времени Δt может быть произвольной, значение отношения (1) в этом случае не зависит от величины этого интервала. Если же поток изменяется более сложным образом, то величина ЭДС не является постоянной, а зависит от времени. В этом случае рассматриваемый интервал времени следует считать бесконечно малым, тогда отношение (1) с математической точки зрения превращается в производную от функции магнитного потока по времени. Математически этот переход полностью аналогичен переходу от средней к мгновенной скорости в кинематике.
 Второе. Понятие потока векторного поля применимо только к поверхности, поэтому необходимо уточнять о какой поверхности идет речь в формулировке закона. Однако, поток магнитного поля через любую замкнутую поверхность равен нулю. Поэтому для двух различных поверхностей, опирающихся на контур магнитные потоки одинаковы. Представьте себе поток жидкости, вытекающий из отверстия. Какую бы вы не выбрали поверхность, границей которого являются границы отверстия, потоки через них будут одинаковы. Здесь уместна еще одна аналогия: если работа силы по замкнутому контуру равна нулю, то работа этой силы не зависит от формы траектории, а определяется только ее начальной и конечной точками.
 Третье. Знак минус в формулировке закона имеет глубокий физический смысл, фактически он обеспечивает выполнение закона сохранения энергии в этих явлениях. Этот знак является выражением правила Ленца. Пожалуй, это единственный случай в физике, когда один знак удостоился собственного имени.
 Как мы показали, во всех случаях физическая сущность явления электромагнитной индукции одинакова и кратко формулируется следующим образом: переменное магнитное поле порождает вихревое электрическое поле. С этой, полевой, точки зрения закон электромагнитной индукции выражается через характеристики электромагнитного поля: циркуляция вектора напряженности электрического поля по любому контуру равна скорости изменения магнитного потока через этот контур

 В этой трактовке явления существенно, что вихревое электрическое поле возникает при изменении магнитного поля, независимо от того, имеется ли реальный замкнутый проводник (контур), в котором возникает ток или нет. Это реальный контур может играть роль прибора, для обнаружения индуцированного поля.
 Наконец, еще раз подчеркнем − электрические и магнитные поля относительны, то есть их характеристики зависят выбора системы отсчета, в которой дается их описание. Однако, этот произвол в выборе системы отсчета, в выборе способа описания не приводит к каким-либо противоречиям. Измеряемые физические величины инвариантны, не зависят от выбора системы отсчета. Например, сила, действующая на заряженное тело со стороны электромагнитного поля, не зависит от выбора системы отсчета. Но при ее описании в одних системах она может трактоваться как сила Лоренца, в других к ней может «добавляться» электрическая сила. Аналогично (даже как следствие) ЭДС индукции в контуре (сила индуцированного тока, количество выделившейся теплоты, возможная деформация контура и т.д.) не зависят от выбора системы отсчета.
 Как всегда предоставляемой свободой выбора можно и необходимо пользоваться − всегда есть возможность выбрать тот метод описания, который вам больше нравится − как наиболее простой, наиболее наглядный, наиболее привычный и т.д.

fizportal.ru