Толяна Ромоданова светлой памяти – ЭСТ: Катюша – любил он эту песню.От проекта dpva.ru, команды Anonimous Freaks, родных, друзей, коллег и одноклассников – некоторые тоже уже ушли от нас R.I.P. Прошло ровно 13 лет. | ||||||
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры. Поделиться:
 Введите свой запрос: | |||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | ||||||
§ 3.3. Основные табличные интегралы
Основные формулы интегрирования
Из
определения интеграла следует, что для
того чтобы проинтегрировать
функцию, нужно найти ее первообразную.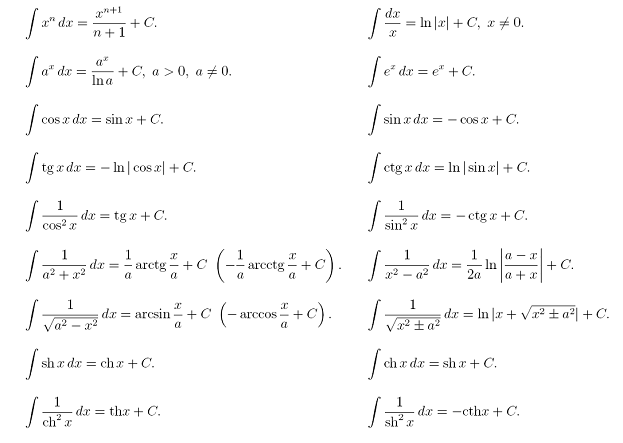
Для ряда функций
это легко сделать, используя соответствующую
формулу
дифференцирования.
Например, мы знаем, что (arcsinx)’ = ; отсюда следует, что = arcsinx +С.
Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.
I. , при n ≠ -1. II. ; III. ;
IV. ; V. ; VI. ; VII. ; VIII. ;
IX. ; X. .
Интегралы, приведенные в этой таблице, называются табличными интегралами.
Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал — подынтегральное выражение.
Формула I справедлива при любом п, кроме п= — 1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл.
Вычисление
интегралов способом приведения их к
табличным с помощью преобразования
подынтегрального выражения и применения
свойств 2 и 3 неопределенного интеграла
называется непосредственным
интегрированием.
При
этом полезно запомнить, что (формула I
при n=0).
Решение. Согласно свойству 2 постоянный множитель 3 вынесем за знак интеграла; получим . Проверка. . Так как получено подынтегральное выражение, то интеграл найден правильно. |
ПОДСТАНОВКОЙ И ПО ЧАСТЯМ
1. Способ подстановки (замены переменной)
2. Способ интегрирования по частям
1. Способ подстановки (замены переменной)
Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).
Заметим,
что все способы интегрирования имеют
целью свести данный интеграл к табличному
с помощью тех или иных искусственных
приемов.
Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить и разделить подынтегральное выражение).
Например, в интеграле ∫sinxcosxdx удобно произвести замену t=sinx, так как оставшаяся часть подынтегрального выражения равна
∫sinx cosxdx = ∫ t dt.
Полученный интеграл является табличным; он находится по формуле I:
∫tdt=1/2 t2 + C.
Далее, произведя обратную замену t = sinx, получим ответ:
½ t2 + C=1/2 sin2x + C.
Решение этого примера можно кратко оформить так:
Напомним, что если при интегрировании одной и той же функции разными способами получили различные результаты, то необходимо показать, что они отличаются на постоянную величину.
Так, рассмотренный выше пример можно решить иначе, если применить формулу sin2х=2sinхcosх. Тогда получим
Результат по виду отличается от найденного ранее; однако, преобразуя первый результат, имеем
Отсюда видно, что разность функций равна 1/4, т. е. постоянному числу.
Естественно возникает вопрос: как правильно выбрать подстановку? Это достигается практикой в интегрировании. Все же можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.
Правило интегрирования способом подстановки состоит в следующем:
1°.
Определяют, к какому табличному интегралу
приводится данный
интеграл (предварительно преобразовав
подынтегральное
выражение, если нужно).
2°. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3°. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4°. Производят замену под интегралом.
5°. Находят полученный интеграл.
6°. В результате производят обратную замену, т. е. переходят к старой переменной. Результат полезно проверить дифференцированием.
Найти неопределенные интегралы способом подстановки. 1) . Решение. Проверка. d(0,1(2x +3)5 +C) = 0,5 (2x + 3)4 (2x)’dx = (2x +3)4dx. 2) Решение. 3) Решение. |
2. Способ интегрирования по частям
При интегрировании функций, содержащих произведения, логарифмы и обратные тригонометрические функции, бывает удобно воспользоваться способом интегрирования по частям.
Выведем формулу интегрирования по частям.
Интегрируя обе части равенства d(uv) = udv + v du, получим
∫d(uv)= ∫udv
откуда ∫udv = uv – ∫vdu. (1)
С помощью формулы (5) нахождение интеграла ∫udv сводится к нахождению интеграла ∫vdu, который может оказаться или проще данного, или даже известным.
При
практическом использовании формулы
интегрирования по частям данное
подынтегральное выражение представляют
в
виде произведения двух сомножителей,
которые обозначают u и dv.
Множитель u стараются
выбрать так, чтобы и’ было
проще, чем и.
1) Решение. Интеграл содержит произведение двух функций х и cosx. Способ подстановки не дает возможности найти этот интеграл. Обозначим х = и, cosxdx = dv; тогда dx = du; v = sinx. Применим формулу интегрирования по частям: Приняв х= и, мы получили и‘= 1 и интеграл ∫vdu оказался проще, чем ∫udv. Если
же в этом интеграле сделать другую
замену: соsх=и, xdx=dv, то
легко убедиться, что полученный
интеграл окажется сложнее исходного,
т. е. замена окажется неудачной. Умение
определить целесообразность
той или иной замены приходит с
приобретением навыка. Иногда формулу интегрирования по частям приходится применять дважды. 2) Решение. Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям: (см. решение примера 1) выше). В результате получаем окончательный ответ: |
Таблица интегралов. Расчет, том 1
Основные интегралы
1. ∫undu=un+1n+1+C,n≠−1∫undu=un+1n+1+C,n≠−1
2. ∫duu=ln|u|+C∫duu=ln|u|+C
3. ∫eudu=eu+C∫eudu=eu+C
4. ∫audu=аулна+C∫audu=аулна+C
5. ∫sinudu=-cosu+C∫sinudu=-cosu+C
6. ∫cosudu=сину+C∫cosudu=сину+C
7. ∫sec2udu=тану+C∫sec2udu=тану+C
8. ∫csc2udu=-cotu+C∫csc2udu=-cotu+C
9. ∫secutanudu=secu+C∫secutanudu=secu+C
10. ∫cscucotudu=-cscu+C∫cscucotudu=-cscu+C
11. ∫tanudu=ln|secu|+C∫tanudu=ln|secu|+C
12.
∫котуду=ln|сину|+C∫котуду=ln|сину|+C
13. ∫secudu=ln|secu+tanu|+C∫secudu=ln|secu+tanu|+C
14. ∫cscudu=ln|cscu-cotu|+C∫cscudu=ln|cscu-cotu|+C
15. ∫dua2−u2=sin−1ua+C∫dua2−u2=sin−1ua+C
16. ∫dua2+u2=1atan−1ua+C∫dua2+u2=1atan−1ua+C
17. ∫duuu2−a2=1asec−1ua+C∫duuu2−a2=1asec−1ua+C
Тригонометрические интегралы
18. ∫sin2udu=12u−14sin2u+C∫sin2udu=12u−14sin2u+C
19. ∫cos2udu=12u+14sin2u+C∫cos2udu=12u+14sin2u+C
20. ∫tan2udu=tanu-u+C∫tan2udu=tanu-u+C
21. ∫cot2udu=-cotu-u+C∫cot2udu=-cotu-u+C
22. ∫sin3udu=−13(2+sin2u)cosu+C∫sin3udu=−13(2+sin2u)cosu+C
23. ∫cos3udu=13(2+cos2u)sinu+C∫cos3udu=13(2+cos2u)sinu+C
24. ∫tan3udu=12tan2u+ln|cosu|+C∫tan3udu=12tan2u+ln|cosu|+C
25. ∫cot3udu=-12cot2u-ln|sinu|+C∫cot3udu=-12cot2u-ln|sinu|+C
26. ∫sec3udu=12secutanu+12ln|secu+tanu|+C∫sec3udu=12secutanu+12ln|secu+tanu|+C
27. ∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C
28.
∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu
29. ∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu
30. ∫tannudu=1n−1tann−1u−∫tann−2udu∫tannudu=1n−1tann−1u−∫tann−2udu
31. ∫cotnudu=-1n-1cotn-1u-∫cotn-2udu∫cotnudu=-1n-1cotn-1u-∫cotn-2udu
32. ∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu
33. ∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu
34. ∫sinausinbudu=sin(a−b)u2(a−b)−sin(a+b)u2(a+b)+C∫sinausinbudu=sin(a−b)u2(a−b)−sin (а+б)и2(а+б)+С
35. ∫cosaucosbudu=sin(a−b)u2(a−b)+sin(a+b)u2(a+b)+C∫cosaucosbudu=sin(a−b)u2(a−b)+sin (а+б)и2(а+б)+С
36. ∫sinaucosbudu=−cos(a−b)u2(a−b)−cos(a+b)u2(a+b)+C∫sinaucosbudu=−cos(a−b)u2(a−b) −cos(a+b)u2(a+b)+C
37. ∫usinudu=sinu-ucosu+C∫usinudu=sinu-ucosu+C
38. ∫ucosudu=cosu+usinu+C∫ucosudu=cosu+usinu+C
39. ∫unsinudu=-uncosu+n∫un-1cosudu∫unsinudu=-uncosu+n∫un-1cosudu
40.
∫ункосуду=унсину-н∫ун-1синуду∫ункосуду=унсину-н∫ун-1синуду
41. 1un+m+n−1n+m∫sinn−2ucosmudu=sinn+1ucosm−1un+m+m−1n+m∫sinnucosm−2udu
Экспоненциальные и логарифмические интегралы
42. ∫ueaudu=1a2(au-1)eau+C∫ueaudu=1a2(au-1)eau+C
43. ∫uneaudu=1auneau-na∫un-1eaudu∫uneaudu=1auneau-na∫un-1eaudu
44. ∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C
45. ∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C
46. ∫lnudu=ulnu-u+C∫lnudu=ulnu-u+C
47. ∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+C∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+ С
48. ∫1ulnudu=ln|lnu|+C∫1ulnudu=ln|lnu|+C
Гиперболические интегралы
49. ∫синхуду=кошу+К∫синхуду=кошу+К
50. ∫кошуду=синху+К∫кошуду=синху+К
51. ∫танхуду=инкошу+К∫танхуду=инкошу+К
52. ∫cothudu=ln|sinhu|+C∫cothudu=ln|sinhu|+C
53. ∫sechudu=tan−1|sinhu|+C∫sechudu=tan−1|sinhu|+C
54.
∫cschudu=ln|tanh22u|+C∫cschudu=ln|tanh22u|+C
55. ∫sech3udu=танху+C∫sech3udu=танху+C
56. ∫csch3udu=−cothu+C∫csch3udu=−cothu+C
57. ∫sechutanhudu=-sechu+C∫sechutanhudu=-sechu+C
58. ∫cschucothudu=-cschu+C∫cschucothudu=-cschu+C
Обратные тригонометрические интегралы
59. ∫sin-1udu=usin-1u+1-u2+C∫sin-1udu=usin-1u+1-u2+C
60. ∫cos-1udu=ucos-1u-1-u2+C∫cos-1udu=ucos-1u-1-u2+C
61. ∫tan−1udu=utan−1u−12ln(1+u2)+C∫tan−1udu=utan−1u−12ln(1+u2)+C
62. ∫usin-1udu=2u2-14sin-1u+u1-u24+C∫usin-1udu=2u2-14sin-1u+u1-u24+C
63. ∫ucos-1udu=2u2-14cos-1u-u1-u24+C∫ucos-1udu=2u2-14cos-1u-u1-u24+C
64. ∫utan−1udu=u2+12tan−1u−u2+C∫utan−1udu=u2+12tan−1u−u2+C
65. ∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1−u2],n≠−1∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1− u2],n≠−1
66. ∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2],n≠−1∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2] ,n≠−1
67. ∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+u2],n≠−1∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+ u2],n≠−1
Интегралы с участием
a 2 + u 2 , a > 0 68.
∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C
69. ∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2)+C∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2 )+С
70. ∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C
71. ∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C
72. ∫dua2+u2=ln(u+a2+u2)+C∫dua2+u2=ln(u+a2+u2)+C
73. ∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C
74. ∫duua2+u2=−1aln|a2+u2+au|+C∫duua2+u2=−1aln|a2+u2+au|+C
75. ∫duu2a2+u2=−a2+u2a2u+C∫duu2a2+u2=−a2+u2a2u+C
76. ∫du(a2+u2)3/2=ua2a2+u2+C∫du(a2+u2)3/2=ua2a2+u2+C
Интегралы с участием
u 2 − a 2 , a > 077. ∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C
78. ∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2|+C∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2 |+С
79.
∫u2−a2udu=u2−a2−acos−1a|u|+C∫u2−a2udu=u2−a2−acos−1a|u|+C
80. ∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C
81. ∫duu2−a2=ln|u+u2−a2|+C∫duu2−a2=ln|u+u2−a2|+C
82. ∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C
83. ∫duu2u2−a2=u2−a2a2u+C∫duu2u2−a2=u2−a2a2u+C
84а. ∫du(u2−a2)3/2=−ua2u2−a2+C∫du(u2−a2)3/2=−ua2u2−a2+C
84б. ∫duu2-a2=12alnu-au+a+C∫duu2-a2=12alnu-au+a+C
Интегралы с участием
a 2 − u 2 , и > 085. ∫a2−u2du=u2a2−u2+a22sin−1ua+C∫a2−u2du=u2a2−u2+a22sin−1ua+C
86. ∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C
87. ∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C
88. ∫a2−u2u2du=−1ua2−u2−sin−1ua+C∫a2−u2u2du=−1ua2−u2−sin−1ua+C
89. ∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C
90.
∫duua2−u2=−1aln|a+a2−u2u|+C∫duua2−u2=−1aln|a+a2−u2u|+C
91. ∫duu2a2−u2=−1a2ua2−u2+C∫duu2a2−u2=−1a2ua2−u2+C
92. ∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+3a48sin−1ua+C∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+ 3a48sin−1ua+C
93а. ∫du(a2−u2)3/2=ua2a2−u2+C∫du(a2−u2)3/2=ua2a2−u2+C
93б. ∫dua2-u2=12alnu+au-a+C∫dua2-u2=12alnu+au-a+C
Интегралы с участием 2
au − u 2 , a > 094. ∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C
95. ∫du2au-u2=cos-1(a-ua)+C∫du2au-u2=cos-1(a-ua)+C
96. ∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C
97. ∫duu2au-u2=-2au-u2au+C∫duu2au-u2=-2au-u2au+C
Интегралы с участием
a + bu , a ≠ 0 98.
∫udua+bu=1b2(a+bu-aln|a+bu|)+C∫udua+bu=1b2(a+bu-aln|a+bu|)+C
99. ∫u2dua+bu=12b3[(a+bu)2−4a(a+bu)+2a2ln|a+bu|]+C∫u2dua+bu=12b3[(a+bu)2−4a(a +bu)+2a2ln|a+bu|]+C
100. ∫duu(a+bu)=1aln|ua+bu|+C∫duu(a+bu)=1aln|ua+bu|+C
101. ∫duu2(a+bu)=−1au+ba2ln|a+buu|+C∫duu2(a+bu)=−1au+ba2ln|a+buu|+C
102. ∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+C∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+ С
103. ∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+C∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+ С
104. ∫u2du(a+bu)2=1b3(a+bu−a2a+bu−2aln|a+bu|)+C∫u2du(a+bu)2=1b3(a+bu−a2a+bu− 2aln|a+bu|)+C
105. ∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C
106. ∫udua+bu=23b2(bu−2a)a+bu+C∫udua+bu=23b2(bu−2a)a+bu+C
107. ∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C
108. ∫duua+bu=1aln|a+bu−aa+bu+a|+C,ifa>0=2−atan−1a+bu−a+C,ifa<0∫duua+bu=1aln|a +bu-aa+bu+a|+C,ifa>0=2-atan-1a+bu-a+C,ifa<0
109. ∫a+buudu=2a+bu+a∫duua+bu∫a+buudu=2a+bu+a∫duua+bu
110.
∫a+buu2du=−a+buu+b2∫duua+bu∫a+buu2du=−a+buu+b2∫duua+bu
111. ∫una+budu=2b(2n+3)[un(a+bu)3/2−na∫un−1a+budu]∫una+budu=2b(2n+3)[un(a+bu) )3/2−na∫un−1a+budu]
112. ∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫un−1dua+bu∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫ ип-1дуа+бу
113. ∫duuna+bu=−a+bua(n−1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu∫duuna+bu=−a+bua(n −1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu
деталей и многое другое | Преподавание исчисления
Этим летом на APSI мы с участниками обсуждали «табличный метод» интегрирования по частям. Поскольку мы далеко ушли от того, что проверяется на экзаменах BC Calculus, я закончил обсуждение и сказал тем, кто заинтересован, я опубликую больше о табличном методе в этом блоге, идущем дальше, чем просто базовая настройка. Так вот.
Вот несколько предыдущих сообщений об интегрировании по частям и табличном методе
Интегрирование по частям 1 описывает основы метода. Это все, что нужно пройти курсу Британской Колумбии.
Интеграция по частям 2 представляет табличный метод.
Модифицированная табличная интеграция представляет собой очень быстрый и удобный способ использования табличного метода без создания таблицы. Это стоит знать.
Также здесь есть видео по интеграции по частям. Прокрутите вниз до «Антипроизводные 5: Тема BC — Интеграция по частям». Табличный метод обсуждается примерно с 15:16. Есть несколько способов сервировки стола; один показан здесь, а немного другой способ — в сообщении «Интеграция по частям 2» выше. Есть и другие.
Идем дальше с табличным методом.Табличный метод хорошо работает, если один из множителей в исходном подынтегральном выражении является многочленом; в конце концов его производная будет равна нулю, и все готово. Они показаны в примерах в сообщениях выше и в Примере 1 ниже. Чтобы завершить тему, в этом посте будут показаны две другие вещи, которые могут произойти при использовании интегрирования по частям и табличного метода.
Сначала мы рассмотрим пример с полиномиальным множителем и научимся останавливаться на полпути.
Зачем останавливаться? Потому что часто не будет конца, если вы не остановитесь. Есть способы завершить интеграцию, как показано в примерах.
Пример 1: Найти табличным методом (подробнее о том, как настроить таблицу, см. в разделе Интеграция по частям 2)
Добавление последнего столбца дает первообразную: остановиться после . Пример 2 показывает, почему вы хотите (нужно) остановиться. В примере 1 у вас будет
Подынтегральное выражение справа — это произведение последнего столбца в строке, на которой вы остановились, и первых двух столбцов в следующей строке, как показано желтым цветом выше.
Пример 2 Найти
Как видите, строки выше иногда повторяются со знаком минус. Однако, если мы остановимся на третьей строке, мы можем написать:
Интеграл в конце идентичен исходному интегралу. Мы можем продолжить, добавив интеграл к обеим частям:
Наконец, мы делим на 2 и получаем первообразную, которую мы пытались найти: может появиться снова, и что делать, если это произойдет.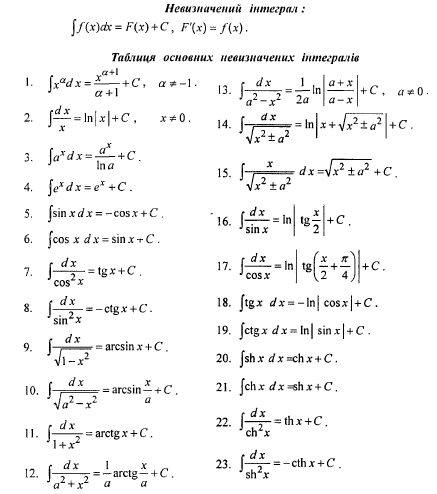
Пока коэффициент не +1, мы можем действовать, как указано выше. То же самое происходит, если мы не используем табличный метод. (Если коэффициент равен +1, то другие члены справа добавятся к нулю, и вам нужно сделать другой выбор для у и дв .)
Еще одно применение интегрирования по частям — получение формул для интегралов со степенями. Получается интеграл, подынтегральная функция которого имеет меньшую степень, чем исходная, но имеет ту же форму. Затем формула повторяется, чтобы постоянно уменьшать степень до тех пор, пока окончательный интеграл не будет легко интегрирован.
Пример 3 : Найти
Пусть
Это формула сокращения; второй интеграл такой же, как и первый, но меньшей степени. Вот как это используется. На каждом шаге подынтегральная функция такая же, как исходная, но на одну ступень ниже. Таким образом, формулу можно применить снова, еще три раза в этом примере.
Большинство учебников содержат краткий набор формул приведения.
Заключительные мысли .Еще в «старые времена» до нашей эры (до появления калькуляторов) начинающие курсы математики много времени уделяли теме «Техники интегрирования». Это включало интегрирование по частям, алгебраические методы, методы, известные как триг-подстановки, и другие. У математиков и инженеров были таблицы интегралов, в которых перечислялось более тысячи форм, и студентов учили, как пользоваться таблицами и различать похожие формы в таблицах. (См. фото ниже из четырнадцатого издания таблиц CRC (c) 1965.) Современные учебники часто содержат такие разделы.
Сегодня в этом нет необходимости. Калькуляторы CAS могут найти первообразные почти любого интеграла. Такие веб-сайты, как WolframAlpha, также доступны для выполнения этой работы.
Не знаю, почему Совет колледжей недавно немного расширил список типов первообразных, проверяемых на экзаменах.